Image Processing Reference
In-Depth Information
(6c)
Why 15(30/2)? Let's assume that the text in an image has some noise around it and the trans-
ition between the color of the text and the color of the background is done through an in-
termediary pixel which could be called “noise pixel” which has a different color. This situ-
ation appears frequently in the real scenarios. Then, the minimum difference of 30 between
the values of the color component of the background and the color component of the text is
spread among three adjacent pixels (background pixel, noise pixel, and text pixel placed as
the colored ones in
Figure 6
)
with three different colors instead of just two adjacent pixels, i.e.,
text pixel and background pixel as in
Figure 7
. For instance, if the intensity of the color of the
background would be (R
b
,G
b
,B
b
) = (0,0,0), the intermediate color (noise color) would have to
be at least (R
n
,G
n
,B
n
) = (0,0,16) and the text color would have to be at least (R
t
,G
t
,B
t
) = (0,0,32),
for the condition in Equation
(6c)
to be fulfilled.
Because of the diagonal manner in which the pixels which contribute to the new value of
the current pixels are placed, meaning that the direction of the gradient is a diagonal direction,
all the noise around curve edges that follow this direction is eliminated. Noise around vertical
and horizontal edges, which form an angle of − 45° and 45° with the diagonal direction, is as
well almost eliminated. Anyway, the noise affects more the curve edges than the horizontal
and vertical edges.
Figure 8
shows the visual representation of all possible cases that fulfill the condition in
Equation
(6c)
, which refers to the Blue component that will be taken as an example further on.
The visual representation for the Red and Green component can be obtained in the same way.
FIGURE 8
Possible cases for the condition in Equation
(6c)
to be fulfilled.
Before geting to the point where a speciic transformation is applied, another condition, in
addition to the one described in Equation
(6c)
, must be first met. The new condition is de-
If the conditions in Equation
(7c)
are fulfilled, then there is a diagonal “blue” gradient. If
component of the current pixel so, therefore, the contrast for the component is increased de-
pending on the result of the comparison with 127(255/2):
(7a)
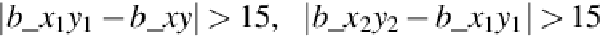

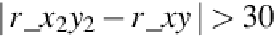
Search WWH ::

Custom Search