Image Processing Reference
In-Depth Information
The second step is to apply
Algorithm 2
with thr and as input data, which divides
into four subsets of 4
γ
− 1
coefficients and adds their significance bits at the end of .
(2)
Sorting Pass
:
Algorithm 3
shows a simplified version of the classification or sorting step of
the H
i
-SET Coder. The H
i
-SET sorting pass exploits the recursion of fractals. If a quadtree
branch is
significant
it moves forward until finding an individual pixel, otherwise the al-
gorithm stops and codes the entire branch as
insigniicant
.
Algorithm 3
is divided into two parts: Sign Coding (lines 2-9) and Branch Significance Cod-
ing (lines 11-16). The algorithm performs
the Sign Coding
by decomposing a given quadtree
branch up to level,
γ
= 0, i.e., the branch is represented by only 4 coefficients with at least
one of them being
significant
. The initial value of
γ
is . Only the
sign of the significant coefficients is coded, 0 for positives and 1 for negatives. Also, each
significant coefficient is added into a spare LSP or LSP′.
The Branch Significance Coding
calls
Algorithm 2
in order to quarter a branch in addition to
call recursively an entire sorting pass at level,
γ
− 1 up to reach the elemental level when,
γ
= 0. The Significance Test results of a current branch (obtained by the
Algorithm 2
)
and
the ones of next branches (acquired by
Algorithm 3
, denoted as
) are added at the end
of
. Also, all the significant coefficients found in previous branches (all the lists LSP′) are
added at the end of the LSP. This process is repeated for all four subsets of
.
ALGORITHM 3
Sorting pass.
(3)
Refinement Pass
: At the end of , the (thr − 1)-th most significant bit of each ordered entry
of the LSP, including those entries added in the last sorting pass, are added. Then, thr is
decremented and another sorting pass is performed. the sorting and refinement steps are
repeated up to thr = 1.
The decoder employs the same mechanism as the encoder, since it knows the fractal applied
to the original image. When the bitstream is received, by itself describes the signiicance
of every variable of the fractal. Then with these bits, the decoder is able to reconstruct both
partially and completely, the same fractal structure of the original image, refining the pixels
progressively as the algorithm proceeds.
4 Experiments and results
For the sake of comparing the performance between the JPEG2000 [
10
] and XSET coders, both
sion with certain viewing conditions is performed, which gives a compressed image with a
particular bit-rate (bpp). Then, a JPEG2000 compression is performed with the same bit-rate.
Once both algorithms recover their distorted images, they are compared with some numerical

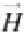




Search WWH ::

Custom Search