Image Processing Reference
In-Depth Information
to start with an
U
trajectory (
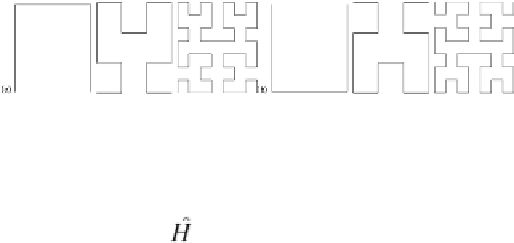
Figure 2(b)
). This proposal is based on the most of the image
energy is concentrated where the higher subbands with lower frequencies are, namely, at
the upper-left quadrant. The first three levels are portrayed in left-to-right order by
Figure
The production rule set of the Hilbert curves is defined as follows:
U
is changed by the
string
LUUR
,
L
by
ULLD
,
R
by
DRRU
and
D
by
RDDL
. In this way, high-order curves are
recursively generated replacing each former level curve with the four later level curves.
The Hilbert Curve process remains in an area as long as possible before moving to the
neighboring region. Hence, the correlation between pixels is maximized, which is an im-
portant image compression issue. Since the higher the correlation at the preprocessing, the
more efficient the data compression.
(b) Axiom = U employed in this chapter.
(2)
Linear Indexing
: A linear indexing is developed in order to store the coefficient matrix into a
vector. Let us define the wavelet transform coefficient matrix as
H
and the interleaved res-
ultant vector as , being 2
γ
× 2
γ
be the size of
H
and 4
γ
'
the size of
H
, where
γ
, is the Hilbert
curve level.
Algorithm 1
generates a Hilbert mapping matrix
θ
with level
γ
, expressing each
curve as four consecutive indexes.
The level
γ
of
θ
is acquired concatenating four different
θ
transformations in the previous
level,
γ
− 1.
Algorithm 1
generates the Hilbert mapping matrix
θ
, where refers a 180° ro-
tation of
β
and
β
T
is the linear algebraic transpose of
β
. Thus, each wavelet coefficient at
H
(
i
,
j
)
is stored and ordered at
, being
θ
(
i
,
j
) the location index into
.
ALGORITHM 1
Function to generate Hilbert mapping matrix
θ
of size 2
γ
× 2
γ
.
(3)
SignificanceTest:
: Asignificance test is defined as the trial of whether a coefficient subset
achieves the predetermined significance level or threshold in order to be a significant or in-
significant It defines how these subsets are formed and what are the coefficients considered
significant
With the aim of recovering the original image at different qualities and compression ratios,
it is not needed to sort and store all the coefficients
but just a subset of them: the subset of
significant coefficients. Those coefficients
H
i
such that are called
significant
other-
wise they are called
insignificant.
. The smaller the
thr
, the beter the inal image quality and the
lower the compression ratio.
Let us define a bit-plane as the subset of coefficients
S
0
such that 2
thr
≤ |
S
0
| ≤ 2
thr + 1
. The sig-
nificance of a given subset
S
0
among a particular bit-plane is store at
and can be deined
as:
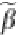
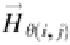


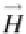
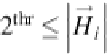
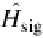
Search WWH ::

Custom Search