Java Reference
In-Depth Information
I⊆{
1
,...,n}
|
I
|
min
(9.3)
such that
i
S
i
=
X.
(9.4)
∈
I
In the literature, the input pair (
X
,
S
) is called a
range space
.
X
3
X
4
X
3
X
4
S
1
X
2
X
2
X
1
X
1
S
3
S
3
S
2
S
7
S
7
X
8
X
8
S
4
S
4
X
5
X
6
X
5
X
6
X
7
X
7
S
6
X
9
X
9
S
5
X
10
X
10
X
11
X
12
X
11
X
12
(a)
(b)
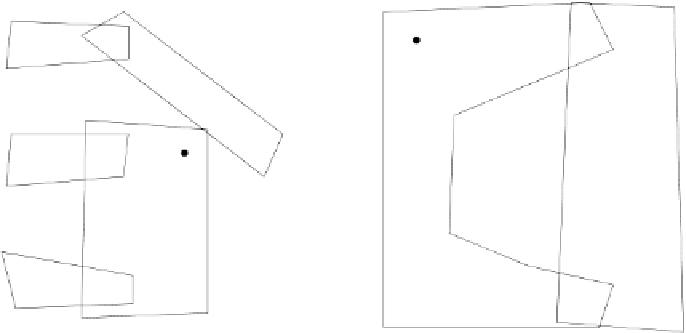
Figure
9.3
Example
of
an
instance
of
a
set
cover
problem:
(a)
input
range
space:
set
X
=
{
X
1
, ..., X
12
}
of
12
elements
and
a
collection
S
=
{{
X
1
,X
2
}
,
{
X
5
,X
6
}
,
{
X
9
,X
10
}
,
{
X
2
,X
8
}
,
{
X
6
,X
7
,X
10
,X
11
}
,
{
of 7 subsets, and
(b) optimal covering of size 3 since elements
X
1
,
X
4
and
X
6
are covered once
by a different subset
X
1
,X
2
,X
3
,X
5
,X
9
,X
10
,X
11
}
,
{
X
3
,X
4
,X
7
,X
8
,X
11
,X
12
}}
As a real-world application of SCP, consider
denoting all grid elements of a
digital terrain, and
S
i
denoting the grid cell covered by the
i
th base transceiver
station. In the telecommunication industry, the goal is to minimize the number
of selected base transceiver stations so that we can fully cover all grid cells
(that is, deserve set
X
). In practice, the problem is relaxed to the partial SCP
by requiring only a fraction of grid cells to be covered, and associating various
costs to selecting this or that base transceiver station. But this does not change
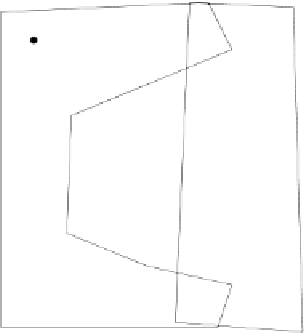
in any way the essence of the SCP. Figure 9.4 displays the result of solving a
(partial) set cover problem for this telecommunication problem on an urban
city scene.
Once again, the greedy heuristic previously sketched yields a simple optimiza-
tion algorithm for finding a covering: We choose the range of
X
S
that covers the
most number of elements of
X
, remove the covered elements from both
X
and
S
all subsets
, and reiterate until none of the grid elements remain. This greedy





















Search WWH ::

Custom Search