Advanced Puzzlers - Java Puzzlers: Traps, Pitfalls, and Corner Cases - page 294

wrong with this code" and "There's obviously nothing wrong with this code." In this case, there's
something very wrong, but it isn't obvious unless you specialize in algorithms.
If you call the shuffle method on an array of length n , the loop iterates n times. In each iteration,
the method chooses one of the n integers between 0 and n - 1. Therefore, there are n n possible
executions of the method. We assumed the random number generator is fair, so each execution
occurs with equal likelihood. Each execution generates one permutation of the array. There is,
however, one small problem: There are n ! distinct permutations of an array of length n . (The
exclamation point after n indicates the factorial operation: n factorial is defined as n x ( n - 1) x ( n -
2) x ...x 1.) The problem is that n n is not divisible by n ! for any n greater than 2, because n ! has
every prime factor from 2 through n , but n n has only the prime factors that make up n . This proves
beyond a shadow of a doubt that the shuffle method generates some permutations more often than
others.
To make this concrete, let's consider an array of length 3 containing the strings "a" , "b" , and "c" .
There are 3 3 = 27 possible executions of the shuffle method. All are equally likely, and each
generates some permutation. There are 3! = 6 distinct permutations of the array: {"a", "b", "c"} ,
{"a", "c", "b"}, {"b", "a", "c"}, {"b", "c", "a"}, {"c", "a", "b"}, and {"c", "b",
"a"} . Because 27 is not divisible by 6, some of these permutations must be generated by more
executions than others, so the shuffle method is not fair.
One problem with this proof is that it offers no intuition into the bias induced by the method; it
merely proves that a bias exists. Often the best way to gain some insight is to perform an
experiment. We ran a program that calculates the expected value of the element at each position
when the method is run on the "identity array," where a [ i ] = i . Loosely speaking, the expected value
is the average value that you'll see in the element if you run the shuffle method repeatedly. If the
shuffle method were fair, the expected value would be the same for each element: (( n -1 ) / 2).
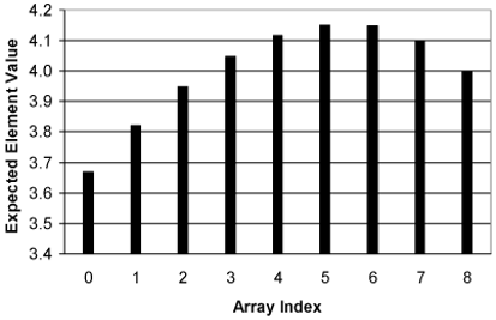
Figure 10.1 shows the expected value for each element in an array of length 9. Note the distinctive
shape of the graph: It starts low, increases beyond the fair value (4), and settles down to the fair
value in the last element.
Figure 10.1. Expected values for the shuffle method on the identity array.