Graphics Reference
In-Depth Information
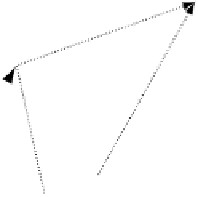
Y
s
h
b
r
X
Fig. 6.12.
The area of the parallelogram formed by two vectors
r
and
s
equals
||
r
|| ·
||
s
||
sin
β
.
6.4 Areas
Before we leave the cross product let's investigate the physical meaning of
r
·
s
sin(
β
). Figure 6.12 shows two 2D vectors,
r
and
s
. The height
h
=
s
sin(
β
), therefore the area of the parallelogram is
||
r
||
h
=
||
r
|| · ||
s
||
sin(
β
)
(6.32)
But this is the magnitude of the cross product vector
t
. Thus when we calcu-
late
r
s
, the length of the normal vector
t
equals the area of the parallelogram
formed by
r
and
s
. Which means that the triangle formed by halving the par-
allelogram is half the area.
×
area of parallelogram =
||
t
||
(6.33)
area of triangle =
1
2
||
t
||
(6.34)
This means that it is a relatively easy exercise to calculate the surface area
of an object constructed from triangles or parallelograms. In the case of a
triangulated surface, we simply sum the magnitudes of the normals and halve
the result.
6.4.1 Calculating 2D Areas
Figure 6.13 shows three vertices of a triangle
P
0
(
x
0
,y
0
)
,P
1
(
x
1
,y
1
)and
P
2
(
x
2
,y
2
)
formed in an anti-clockwise sequence. We can imagine that the triangle exists
on the
z
= 0 plane, therefore the
z-coordinates
are zero.