Graphics Reference
In-Depth Information
Y
X
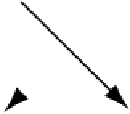
Fig. 6.3.
Eight vectors, whose coordinates are shown in Table 6.1.
(
x
t
,y
t
) respectively, its components ∆
x
and ∆
y
are given by
∆
x
=(
x
h
−
x
t
)
y
=(
y
h
−
y
t
)
(6.1)
One can readily see from this notation that a vector does not have a unique
position in space. It does not matter where we place a vector: so long as we
preserve its length and orientation, its components will not alter.
6.1.3 Magnitude of a Vector
The
magnitude
of a vector
r
is expressed by
r
and is computed by applying
the theorem of Pythagoras to its components:
=
∆
x
2
+∆
y
2
||
r
||
(6.2)
To illustrate these ideas, consider a vector defined by (
x
h
,y
h
)=(3
,
4) and
(
x
t
,y
t
)=(1
,
1). The
x
-and
y
-comp
onents are 2 and 3 respectively. Therefore
its magnitude is equal to
√
2
2
+3
2
=3
.
606
Figure 6.3 shows various vectors, and their properties are listed in
Table 6.1.
6.2 3D Vectors
The above vector examples are in 2D, but it is extremely simple to extend
this notation to embrace an extra dimension. Figure 6.4 shows a 3D vector
r
with its head, tail, components and magnitude annotated. The components
and magnitude are given by
∆
x
=(
x
h
−
x
t
)
(6.3)