Cartesian Coordinates - Mathematics for Computer Graphics - page 26

Y

P 2

y 2
∆

d

y

P 1

y 1

x 1 x 2

∆ x

X

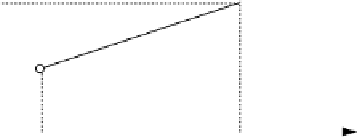
Fig. 5.4. Calculating the distance between two points.

As a simple test, let's apply (5.1) to the shape described in Figure 5.3:

1
2 [(1

× 1 − 3 × 1) + (3 × 2 − 3 × 1) + (3 × 3 − 1 × 2) + (1 × 1 − 1 × 3)]

1
2 [

− 2+3+7 − 2] = 3

which by inspection, is the true area. The beauty of this technique is that it
works with any number of vertices and any arbitrary shape. In Chapter 6 we
will discover how it works.
Another feature of the technique is that if the original set of coordinates
is clockwise, the area is negative. Which means that the calculation computes
vertex sequence as well as area. To illustrate this feature, the original vertices
are reversed to a clockwise sequence as follows:

1
2 [(1

× 3 − 1 × 1) + (1 × 2 − 3 × 3) + (3 × 1 − 3 × 2) + (3 × 1 − 1 × 1)]

1
2 [2

− 7 − 3+2]= − 3

The minus sign indicates that the vertices are in a clockwise sequence.

5.1.5 Theorem of Pythagoras in 2D

We can calculate the distance between two points by applying the theorem of
Pythagoras. Figure 5.4 shows two arbitrary points P 1 ( x 1 ,y 1 )and P 2 ( x 2 ,y 2 ).
The distance ∆ x = x 2 − x 1 and ∆ y = y 2 − y 1 Therefore, the distance d between

P 1 and P 2 is given by

d = ∆ x 2 +∆ y 2 (5.2)