Graphics Reference
In-Depth Information
interpolant, we require an interpolated value controlled by a parameter
t
that
varies between 0 and 1. When
t
= 0, the result is
n
1
,andwhen
t
=1,the
result is
n
2
. A solution to this problem is given by
n
=
n
1
+
t
(
n
2
−
n
1
)
(8.1)
for when
n
1
=2
,n
2
=4and
t
=0
.
5
n
=2+
1
2
(4
−
2) = 3
which is a halfway point. Furthermore, when
t
=0
,n
=
n
1
,andwhen
t
=
1
,n
=
n
2
, which confirms that we have a sound interpolant. However, it can
be expressed differently:
n
=
n
1
+
t
(
n
2
−
n
1
)
(8.2)
n
=
n
1
+
tn
2
−
tn
1
(8.3)
n
=
n
1
(1
−
t
)+
n
2
t
(8.4)
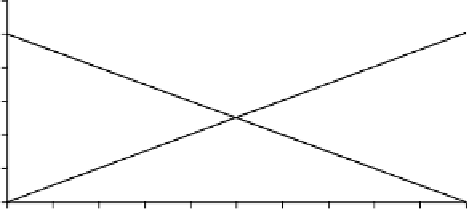
which shows what is really going on, and forms the basis for further
development. Figure 8.1 shows the graphs of (1
−
t
)and
t
over the range
0to1.
With reference to (8.4), we see that as
t
changes from 0 to 1, the (1
t
)term
varies from 1 to 0. This effectively attenuates the value of
n
1
to zero over the
range of
t
, while the
t
term scales
n
2
from zero to its actual value. Figure 8.2
illustrates these two actions with
n
1
=1and
n
2
= 3. Notice that the terms
(1
−
t
)and
t
sum to unity; this is not a coincidence. This type of interpolant
ensures that if it takes a quarter of
n
1
, it balances it with three-quarters of
n
2
,
and vice versa. Obviously we could design an interpolant that takes arbitrary
portions of
n
1
and
n
2
, but that would lead to arbitrary results. Although
this interpolant is extremely simple, it is widely used in computer graphics
software. Just to put it into context, consider the task of moving an object
−
1.2
1
(1
−
t
)
t
0.8
0.6
0.4
0.2
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t
Fig. 8.1.
The graphs of (1
− t
) and t over the range 0 to 1.