Graphics Reference
In-Depth Information
Figure 22.1.
Properties of maps with respect to iteration.
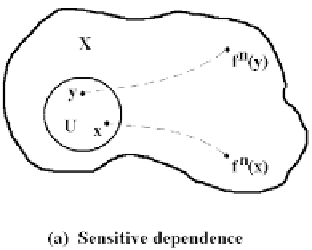
Saying that a map f has sensitive dependence on initial conditions means that
there are points arbitrarily close to any given point
x
which separate from
x
by some
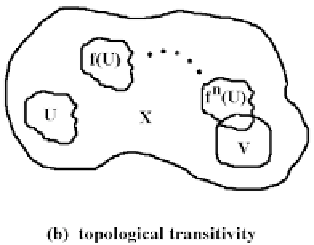
fixed d under iterations of f. See Figure 22.1(a). Saying that a map f is topologically
transitive means that every neighborhood has points that are eventually moved into
any other neighborhood under iterates of the map. See Figure 22.1(b). If all orbits are
dense, then the map is topologically transitive. The converse is true for compact
subsets of
R
or
S
1
.
The definition of a chaotic map is the well-known definition from [Deva86]. It
turns out however that conditions (1)-(3) in the definition are not independent. It is
shown by Banks et al. ([BBGDS92]) that conditions (2) and (3) imply (1), so that being
chaotic is a purely topological property and does not depend on a metric. Further,
Vellekoop and Berglund ([VelB94]) proved that in the case of connected subsets of
R
condition (2) implies (3). They also showed that (1) and (3) do not imply (2). Nor do
(1) and (2) imply (3). Therefore, for connected sets of
R
, a map is chaotic if and only
if it satisfies condition (3) alone. It follows that the essential condition is topological
transitivity. Crannell ([Cran95]) looks at alternatives to that condition that are more
intuitive.
Chaotic maps are maps that we would prefer not to have to deal with, but some
very simple maps are chaotic.
22.2.1 Example.
If we parameterize the points of the unit circle by the angle they
make with the x-axis, then the map
1
1
fS
:
Æ
()
qq
S
f
2
is chaotic. Any small arc eventually covers all of the circle, some points move apart,
and the periodic points are dense.
22.2.2
Example.
Another simple chaotic map is the map
[
Æ
[]
()
=
f
fx
:,
01 01
41
,
.
(
)
x
-
x