Graphics Reference
In-Depth Information
1
2
1
2
p
i
nt
Ú
()
-
i
nt
a
=<
f e
,
> =
f t e
dt
.
(21.11)
n
[
-
pp
,
]
p
p
p
In any case,
Definition.
The a
n
defined by (21.11) are called the
Fourier coefficients
of f and the
series (21.10) is called the
Fourier series
for f (with respect to the functions e
int
).
The Fourier coefficient a
n
intuitively says how much of the function e
int
appears
in f.
Since
i
nt
e
=
cos
nt
+
i
sin
nt
,
the Fourier series for real functions is easily shown to be expressible in the form
•
Â
a
0
(
)
+
a
cos
t
+
b t
sin
,
(21.12)
n
n
2
n
=
1
where
1
1
p
p
Ú
()
Ú
()
a
=
f t
cos
ntdt
and
b
=
f t
sin
ntdt
.
(21.13)
n
n
p
p
-
p
-
p
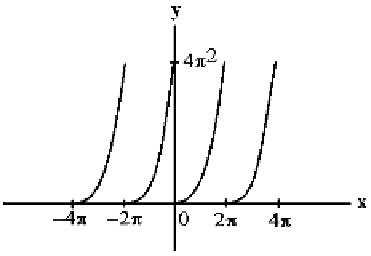
21.5.2 Example.
Consider the function f(x) = x
2
on the interval (0,2p) and think of
it as a periodic function defined on the reals as shown in Figure 21.4. Then, carrying
out the relevant integrations using standard formulas for trigonometric integrals, the
Fourier series for f is found to be
•
Â
2
4
p
4
4
p
È
Í
˘
˙
+
cos
nx
-
sin
nx
.
3
2
n
n
n
=
1
See [Spie69] for this and other examples.
Figure 21.4.
The function f(x) of Exercise
21.5.2.