Graphics Reference
In-Depth Information
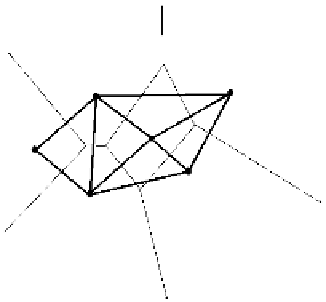
Figure 17.16.
A Delaunay triangulation.
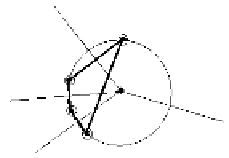
Figure 17.17.
A nontriangular face of a Delaunay cell complex.
Definition.
Let
S
be a finite set of points (sites) in the plane. The
Delaunay graph
of
S
is the graph with vertex set
S
and whose edges are defined by the condition that
two vertices are connected by an edge if and only if the Voronoi cells associated
to those vertices share a common edge. The
Delaunay cell complex
of
S
is the two-
dimensional cell complex defined by the condition that its vertices and edges are the
vertices and edges of the Delaunay graph of
S
. The 2-cells are called the
faces
of the
Delaunay cell complex. By subdividing the faces of the Delaunay cell complex into tri-
angles, if they are not that already, one obtains a two-dimensional simplicial complex
called a
Delaunay triangulation
of
S
.
Figure 17.16 shows the Delaunay cell complex associated to the Voronoi diagram
in Figure 17.14. As we can see, it is in fact a Delaunay triangulation. Figure 17.17
shows a Delaunay cell complex defined by the four sites marked by circles. It consists
of a single face that is a quadrilateral and not a triangle. It admits two Delaunay
triangulations. Now, the fact that we always do get a real cell complex needs some
justification, which is provided by the properties of the Delaunay graph listed in the
following theorem.
17.8.1
Theorem.
The Delaunay graph for a set
S
satisfies the following properties:
(1) The Delaunay graph G is the “dual graph” of the Voronoi diagram D in the
sense that a Voronoi cell in D becomes a vertex in G, an edge
e
in D defines an edge
in G between the two vertices in G that correspond to the Voronoi cells that have
e
in common, and a vertex
v
in D defines the (triangular) region bounded by edges of
G which connect the Voronoi cells that have
v
in common. (Compare this to the
barycentric subdivision of a simplicial complex.)