Graphics Reference
In-Depth Information
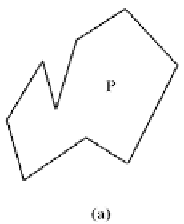
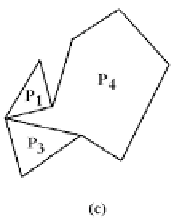
Figure 17.12.
Finding y-monotone regions of a polygon.
structures such as a priority queue and balanced search trees to optimize the opera-
tions in the algorithm, one can prove the following.
17.6.3 Theorem.
A polygon with n vertices can be partitioned into y-monotone
regions in O(n log n) time using O(n) storage.
Proof.
See [BKOS97].
The next step is to find an efficient algorithm for triangulating a y-monotone
polygon. The idea of such an algorithm is to walk down along the right and left part
of the boundary of the polygon starting from a highest vertex, adding diagonals as we
go along using a greedy type algorithm. Algorithm 17.6.1 sketches the main steps for
the case of a strictly y-monotone polygon.
Definition.
A y-monotone polygon is said to be
strictly y-monotone
if it does not have
any horizontal edges.
At any rate, the complexity of Algorithm 17.6.1 is clearly linear in the number of
vertices of the polygon, so that we get.
17.6.4
Theorem.
A strictly y-monotone polygon with n vertices can be triangulated
in O(n) time.
Proof.
See [BKOS97].
Fortunately, although the y-monotone polygons obtained from Theorem 17.6.3
may not be strictly y-monotone, they are good enough so that Algorithm 17.6.1 works
on them also and so Theorems 17.6.3 and 17.6.4 lead to the following result:
17.6.5
Corollary.
A polygon with n vertices can be triangulated in O(n log n) time
using O(n) storage.
Corollary 17.6.5 is not the best that one can do. Chazelle ([Chaz91]) has shown
that one can triangulate polygons in linear time; however, the argument is rather com-
plicated. Other references for the (simple) polygon triangulation problem are
[Orou94] and [NarM95]. In some applications, such as finite element analysis, one is
not satisfied with just any triangulation. In particular, skinny triangles or triangles