Graphics Reference
In-Depth Information
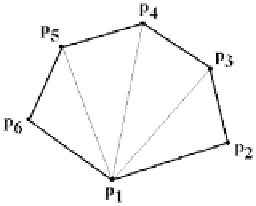
Figure 17.8
Triangulating a convex polygon.
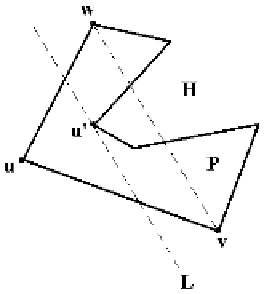
Figure 17.9.
Finding a diagonal of a polygon.
thought of as being defined by a sequence of vertices. Polygons have
no
holes and
they are not “self-intersecting.” Some texts, such as [BKOS97], call such polygons
simple polygons
.
The approach to triangulating an arbitrary (simple) polygon will be to successively
add edges between two of its vertices.
Definition.
A
diagonal
of a polygon
P
is a segment (1-simplex)
uv
between two dis-
tinct vertices
u
and
v
of
P
whose interior is contained in the interior of
P
.
In Figure 17.8 the segment
p
1
p
3
is a diagonal, but
p
1
p
2
is not. A segment between
two vertices that passes outside of the polygon, which could happen if it is not convex,
is not a diagonal.
Every polygon
P
in
R
2
with n > 3 vertices has a diagonal.
17.6.1
Lemma.
Proof.
Order the vertices of
P
by their x-coordinates and, of the left-most vertices,
let
u
be the one with the smallest y-coordinate. Let
v
and
w
be the two vertices of
P
adjacent to
u
. See Figure 17.9. If
vw
is a diagonal, then we are done. Otherwise, let
S be the set of all vertices of
P
other than
u
,
v
, and
w
that lie in the triangle
uvw
.
Choose a vertex
u
¢ in S that is farthest from the line through
v
and
w
. We claim that
uu
¢ is a diagonal. This is because if
L
is the line through
u
¢ that is parallel to
vw
, then
the halfplane
H
defined by
L
, which does not contain
u
is convex and must contain
all the points of S and any edges of
P
between these points.