Graphics Reference
In-Depth Information
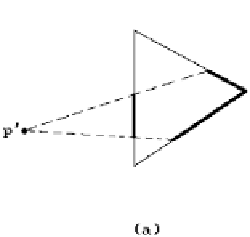
Figure 15.9.
Limiting the number of children of a node.
shadows can cover angles opposite an edge and this would give rise to two children
to a node. However, our task was to find shortest paths and not all geodesics. Because
of this it turns out that the initial edge sequence tree can be pruned. The key obser-
vation is that at most one node whose shadows cover the angle needs to be given two
children if one is only looking for shortest paths. See Figure 15.9(b). In the figure
nodes N
1
and N
2
with the same edge
BC
gave rise to unfolded start points
p
1
and
p
2
with respect to face
ABC
. If |
p
1
A
|<|
p
2
A
|, then the shorter paths to
s
from points on
edges
AB
and
AC
sufficiently close to
A
come from the edge sequence defined by N
1
.
This means that only N
1
needs to be given two children. If |
p
1
A|=|
p
2
A|, then both N
1
and N
2
need only one child. Using this “one angle, one split” criterion leads to a new
edge sequence tree generation algorithm that produces a tree with O(n) leaves at each
stage. One can reduce the total space used to O(n) by the following trick: if a leaf in
the current tree generates only one child, we delete that node and replace it with the
child. One can also show that the new tree can be generated in time O(n
2
). Once the
tree is built, one can find shortest paths in time O(n). To do better, one needs to make
some more improvements.
It turns out that the essential information one needs to store is the shortest paths
to vertices. Therefore, the authors in [CheH90] create additional “vertex nodes” while
they build the edge sequence tree. This can also be done using O(n) space and, given
the nature of the tree, one can now find the shortest path to a
vertex
in time O(k),
where k is the number of edges in the path.
Now the edge sequence tree certainly has to be built once. This takes time O(n
2
).
However, after that, what slows down answering shortest path queries to O(n) is
finding path information in the tree. By storing that information more efficiently one
can speed up multiple queries. An appropriate Voronoi diagram and the subdivision
it induces on the surface turns out to do the trick.
First, one cuts the surface along the shortest paths to its vertices. The cut surface
can be flattened out into the plane (there may be overlaps). The authors in [CheH90]
call the layout one gets the
inward layout
to distinguish it from the one used in
[ShaS86]. The start point
s
will map to O(n) vertices
s
¢. A Voronoi diagram is built
with respect to these image points in the plane and this induces a subdivision of the
layout with the property that points that belong to the same region, say the one asso-
ciated to
s
¢, are closer to
s
¢ than to any other
s
¢, i π j, and their shortest paths have
the same edge sequence. This leaves the question of the complexity of building the
Voronoi diagram. Lemma 15.3.2.5(2) implies that all vertices other than the start point