Graphics Reference
In-Depth Information
Figure 15.7.
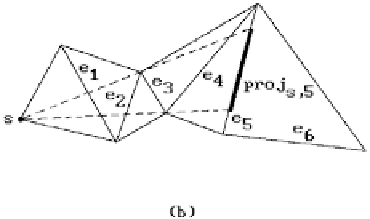
Regions with the same edge sequence.
Figure 15.8.
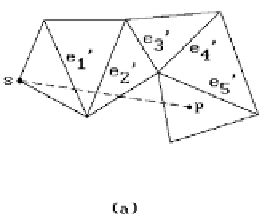
Impossible and possible edge sequences for shortest curves.
15.3.2.4
Lemma
(1) A discrete geodesic is a curve that alternates between vertices and (possibly
empty) edge sequences such that the unfolded path along any edge sequence is a
straight line segment. If the curve passes through any surface vertex, then the angle
that the curve makes at that vertex is greater than or equal to p.
(2) If a discrete geodesic between two points is actually the shortest curve between
those points, then no edge can appear in more than one edge sequence and each edge
sequence must be simple.
Proof.
See [MiMP87]. Figure 15.5(b) shows how a sequence of vertices could be part
of a geodesic.
The basic idea that will lead to our main theorem (Theorem 15.3.2.6) is to divide
the surface into regions, so that the shortest pwl curves from the start point
s
to all
the points within a region define the same edge sequence. See the shaded region in
Figure 15.7.
Definition.
If p is a shortest pwl curve from
s
to a point
p
that defines an edge
sequence, then that edge sequence will be called a
shortest edge sequence for
p
.
Not every edge sequences is a shortest edge sequence. For example, if we are
dealing with a convex surface in Figure 15.8(a), then the unfolded edge sequence
e
1
,
e
2
,
e
3
,
e
4
,
e
5
cannot possibly come from a shortest edge sequence. (It could be without
the hypothesis of convexity as one can see from Figure 15.5(b).) In the next stage of
our discussion we shall assume that surfaces are
convex
. The following facts hold in
that case: