Graphics Reference
In-Depth Information
Tracing directions (
-
f
y
,f
x
) for f(x,y)
=
y
2
-
x
2
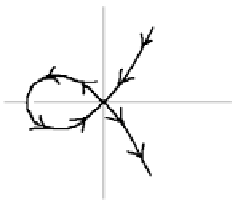
Figure 14.25.
-
x
3
.
If this is not true, then we need to trace the parameterization in the negative t direc-
tion. From this we see that the issue of the tracing direction of a curve involves the
following two points:
(1) The direction in which we trace is not determined intrinsically by a curve
C
but by the function f which is used to define it. If we replace f by -f, then the
curve will be traced in the opposite direction.
(2) In addition to finding a parameterization for the curve, we need to check d
f,g
,
which determines whether the parameter t induces the same direction as the
one in which we want to trace.
If the curve we are tracing has no singularities, then no more needs to be said. If
singularities exist, in particular if the origin is a singularity, then the standard tracing
directions may not vary continuously as we pass through the origin. We can see this
in Figure 14.25 ([Hoff89]). Of course in that case we do not trace the curve using the
function f alone but use a transform g of it to get past the singularities. Tracing g will,
just like in the case of f, involve the gradient of g and a parameterization of g. We
need to establish how the tracing direction of g should be determined from that of f.
Assuming that a
0
π 0, so that we can use a T
1
transformation, then g(u,v) = f (T
1
-
1
(u,v)), and so by the chain rule Dg = Df
°
DT
1
-1
. If (u,v) = T
1
(x,y), then
10
)
Ê
Ë
ˆ
¯
—
(
)
=
(
(
)
(
)
guv
,
f xy
,
f xy
,
x
y
vu
xf
+
yf
Ê
Á
ˆ
˜
x
y
(14.15)
=
x
,
f
.
y
2
x
The parameterization for g at (u,v) induced by g is
()
=
()
ut
xt
()
()
=+ +
yt
xt
()
=
01 2
2
vt
cct
ct
+
...
It is easy to show by long division that
b
a
0
0
c
=
0