Graphics Reference
In-Depth Information
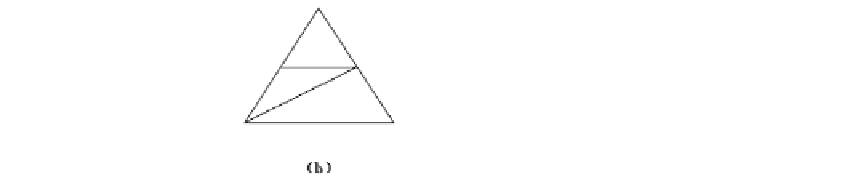
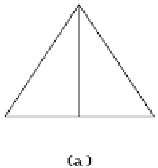
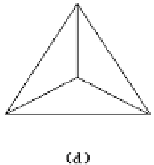
Figure 14.8.
Possible triangle subdivisions.
(3) If the patch passes both the curve and surface flatness test, then output the
planar triangle defined by the three corner vertices.
When subdividing triangles one has several choices. See Figure 14.8. The curve flat-
ness test basically was to check if the Bézier control points
p
0
,
p
1
,...,
p
n
for any edge
are sufficiently close to the segment [
p
0
,
p
n
]. The surface flatness test was similar. One
checked if the Bézier control points for a patch with corner control points
q
0
,
q
1
, and
q
2
are close enough to the planar triangle
q
0
q
1
q
2
. Crack prevention was based on the
approach in [BaDD87].
A further subdivision algorithm can be found in [FiMM86]. It determines the
fineness of the subdivision based on computing bounds for the derivatives of the C
2
parameterizing functions, so that one can also specify the accuracy of the linear
approximation. It produces right triangles in the parametric domain and cracks
between neighboring patches. The subdivision is not adaptive, but the authors claim
that it is several times faster than the adaptive algorithms in [LanR80] and [Fili86].
The adaptive algorithm by Herzen and Barr ([HerB87]) produced a triangulation
using a quadtree for parameter space based on curvature bounds. One again got right
triangles in parameter space and a potentially large number of triangles with cracks
between patches.
We mention two more papers with a slightly different flavor. Cuillière ([Cuil98])
describes an automatic mesh generation algorithm useful for finite element mesh gen-
eration where one is given some a priori nodal density function that might have been
obtained from some knowledge of the object's features. This approach differs from
the more usual approach where one starts with nodes that are a crude approximation
and then refines them as needed. Here we already have some information about where
the nodes should be. Volpin et al. ([VSBJ98]) start with a smooth model and want to
produce another model that is within a given tolerance of the original one but that is
based on a simpler facet structure. The problem can be considered to be an example
of the model simplification problem that we shall describe later. The algorithm in the
paper first divides the input model into regions over which a discrete curvature related
value is within a specified range. Next, a quadrilateral mesh is defined from those
regions and finally a smooth surface is constructed for this mesh. The mesh is well
suited for finite element analysis.
The majority of the early work on polygonizing curves and surfaces involved
various types of recursive subdivisions of the parameter space. [HerB87] gives a good
overview of this approach along with references. A quadtree type data structure was
a major ingredient in the surface case. A more direct approach is described by Kosters