Graphics Reference
In-Depth Information
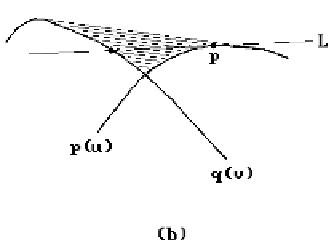
Figure 13.4.
Curve intersections with the Newton-Raphson method.
Let v
0
be a solution. Now find the intersection of the tangent line
L
1
to q(v) at
p
1
= q(v
0
) with the curve p(u). Let this point be
p
2
= p(u
1
).
(3) Continue this process, getting sequences u
i
, v
i
, and
p
i
. Stop when |
p
i
-
p
i+1
| is
sufficiently small.
See Figure 13.4(a). The method works as long as the tangents keep intersecting the
curves. In Figure 13.4(b) this corresponds to starting at points along the boundary of
the shaded region.
Numerical techniques for tracing curves work pretty well if one does not run into
any singularities. The problem at singularities is that the approximation that one is
using for the curve fails to be sufficiently accurate at such points.
13.3.4
Curve Recursive Subdivision Methods
We can extend the line-curve recursive subdivision (divide-and-conquer) approaches
described earlier. The only difference is that we keep subdividing both curves and
checking for intersections of bounding boxes. For curves that satisfy the variation
diminishing property we get the algorithm from [LanR80]. The algorithm in
[KopM83] applies to arbitrary curves.
The paper [SedN90] describes a better algorithm for planar Bézier curves. The
authors refer to their approach as
Bézier clipping
. It is also a bounding box type
approach.
Definition.
A
fat line
is the region between two parallel lines.
Note that a fat line can be thought of as special case of the slabs defined in Section
6.2. The reader should compare the computations we will make for fat lines with those
we made for slabs. Some other related concepts are the “fat arcs” in [SeWZ89], used
as a criterion for curve flatness, and what could be called “fat planes”, used in [Carl82]
for an intersection algorithm for Bézier surfaces.
The first thing we want to do is associate a fat line to an arbitrary Bézier curve
p(u). Let
p
i
= (x
i
,y
i
), i = 0,1, . . . n, be the control points of p(u). See Figure 13.5. Let
L
be the line through
p
0
and
p
n
. Represent the line by an equation of the form