Graphics Reference
In-Depth Information
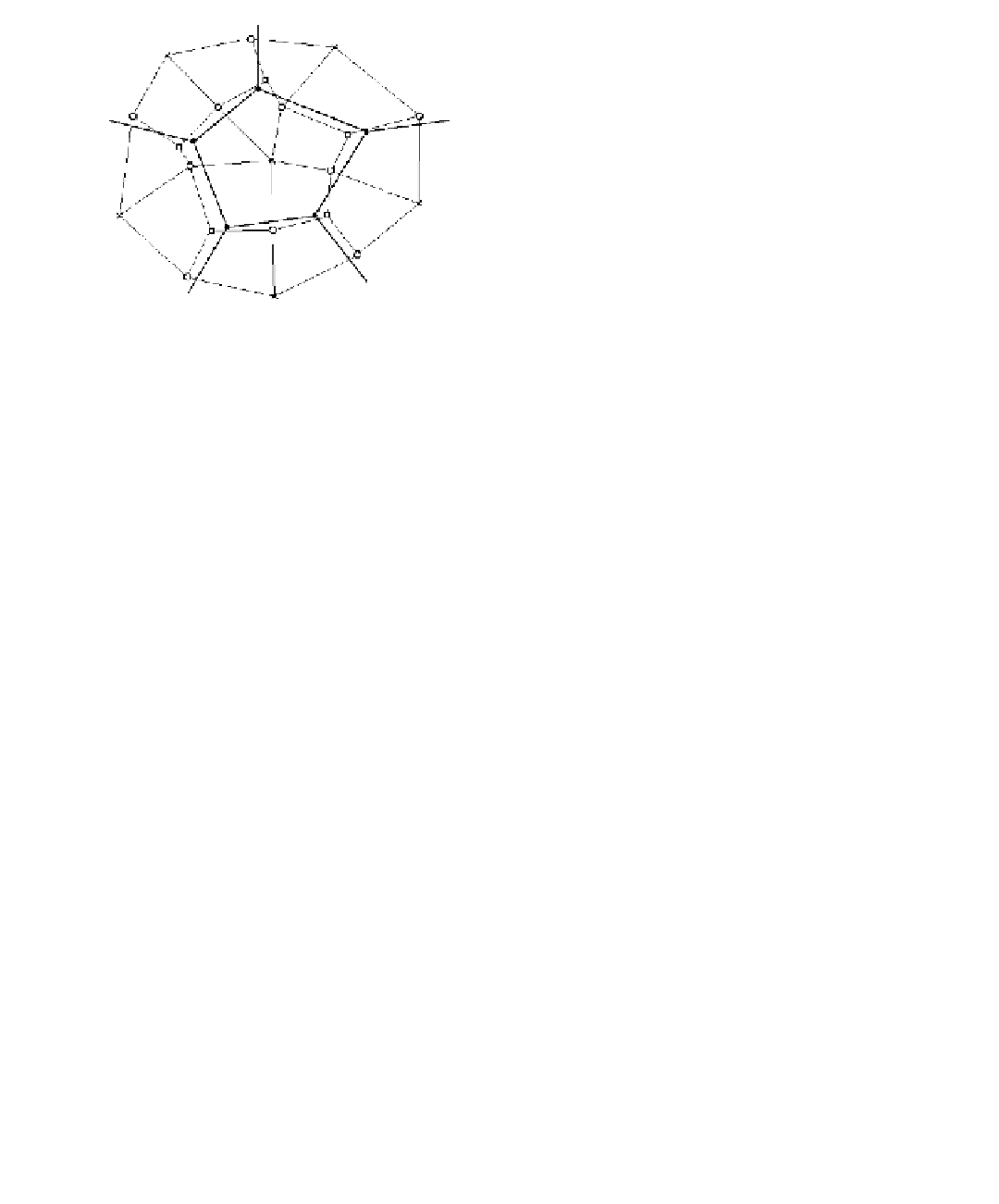
Figure 12.30.
Catmull-Clark subdivision
surface.
unbounded results when trying to estimate the curvature there or the curvature may
be zero.
A final subdivision algorithm we would like to mention is the Loop algorithm
([Loop87]). This is another vertex insertion algorithm that produces a triangular mesh
and a similar C
2
parameterization. Details of the algorithm can also be found in
[Gall00].
The limit surfaces that one gets from subdivision algorithms like the ones discussed
in this section are often called
recursive subdivision surfaces
. It is shown in [Stam98]
and [ZorS99] that points and derivatives of Catmull-Clark and Loop limit surfaces can
be computed directly without subdividing. The advantage of vertex insertion algo-
rithms is that there is a natural way to associate the vertices of the original surface with
vertices of the subdivided surface. For a more thorough discussion of the advantages
and disadvantages of various subdivision schemes see [ZorS99]. For subdivision sur-
faces that interpolate a given set of possibly intersecting curves see [Nasr00].
12.18
Summary for Curves and Surfaces
In the last two chapters we have covered a great many topics on curves and surfaces.
However, anyone wanting to develop a modeling system would quickly find that they
have been presented with lots of choices. The intent of this section is to discuss some
of the hard decisions that inevitably have to be made with regard to questions such
as the following:
(1) What types of curves and surfaces should be supported?
(2) What sort of mathematical functions should be used for the parameteriza-
tions?
(3) Which algorithms should be used to compute values and derivatives for the
chosen types?
Constructing curves and especially surfaces is not an easy task and so a user would
want a modeling system to support as wide a range of curve and surface construc-