Graphics Reference
In-Depth Information
triangular meshes and whether they approximate or interpolate. An important ques-
tion for all these algorithms is whether repeated application produces a sequence of
surfaces that converges to a surface and how smooth this limit surface is. See [Reif95].
The first subdivision algorithm that we shall describe is the Doo-Sabin algorithm
([DooS78]). This algorithm is a corner-cutting algorithm and is a generalization of the
Chaikin curve subdivision algorithm that we described in Section 11.14. The Doo-Sabin
algorithm starts with a polygonal surface
S
that has been defined by a set of vertices
together with a specification of its edges and faces. (Actually, the faces do not need to be
planar for the algorithm and all we need is a polygon-type data structure and not a real
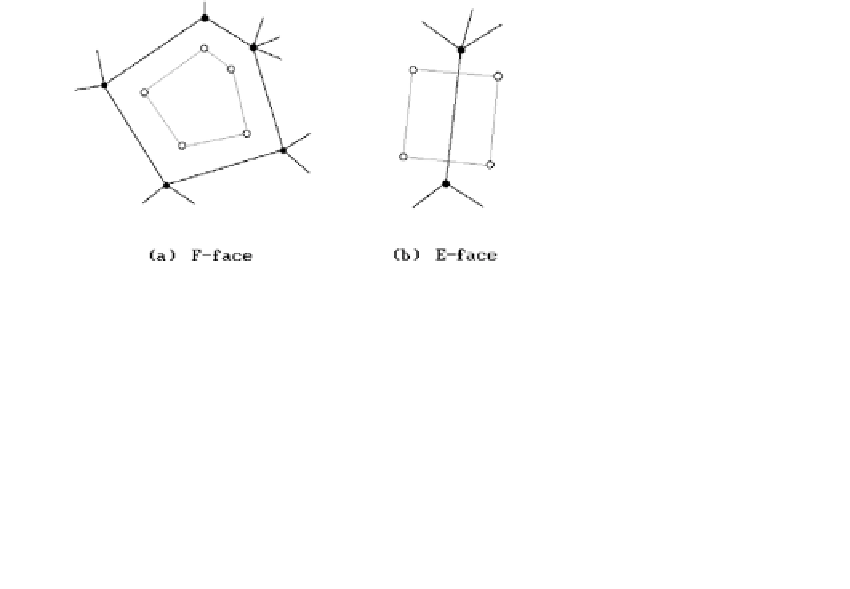
polygon.) One then defines some new vertices for each face
F
, one for each vertex of
F
,
and this new set of vertices will then become the vertex set of the subdivided surface
S
¢.
The faces (and edges) of
S
¢ are determined by the following three rules:
(1) If
F
was an n-sided face of
S
, then the n new vertices associated to
F
will
become a face of
S
¢ and is called an
F-face
. See Figure 12.29(a).
(2) If
E
is an edge of
S
that belongs to faces
F
and
F
¢ of
S
, then the four vertices
of
S
¢ created for the endpoints of
E
in
F
and
F
¢ define a face of
S
¢ called an
E-face
. See Figure 12.29(b). No face is associated to a boundary edge of
S
.
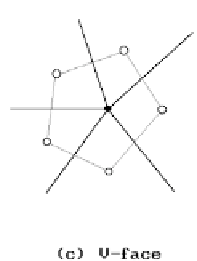
(3) If
V
is a nonboundary vertex of
S
that belonged to n faces of
S
, then the n ver-
tices of
S
¢, associated to the vertex
V
in those n faces, define a face of
S
¢ called
an
V-face
. See Figure 12.29(c).
Figure 12.29.
The new vertices of the Doo-Sabin algorithm.