Graphics Reference
In-Depth Information
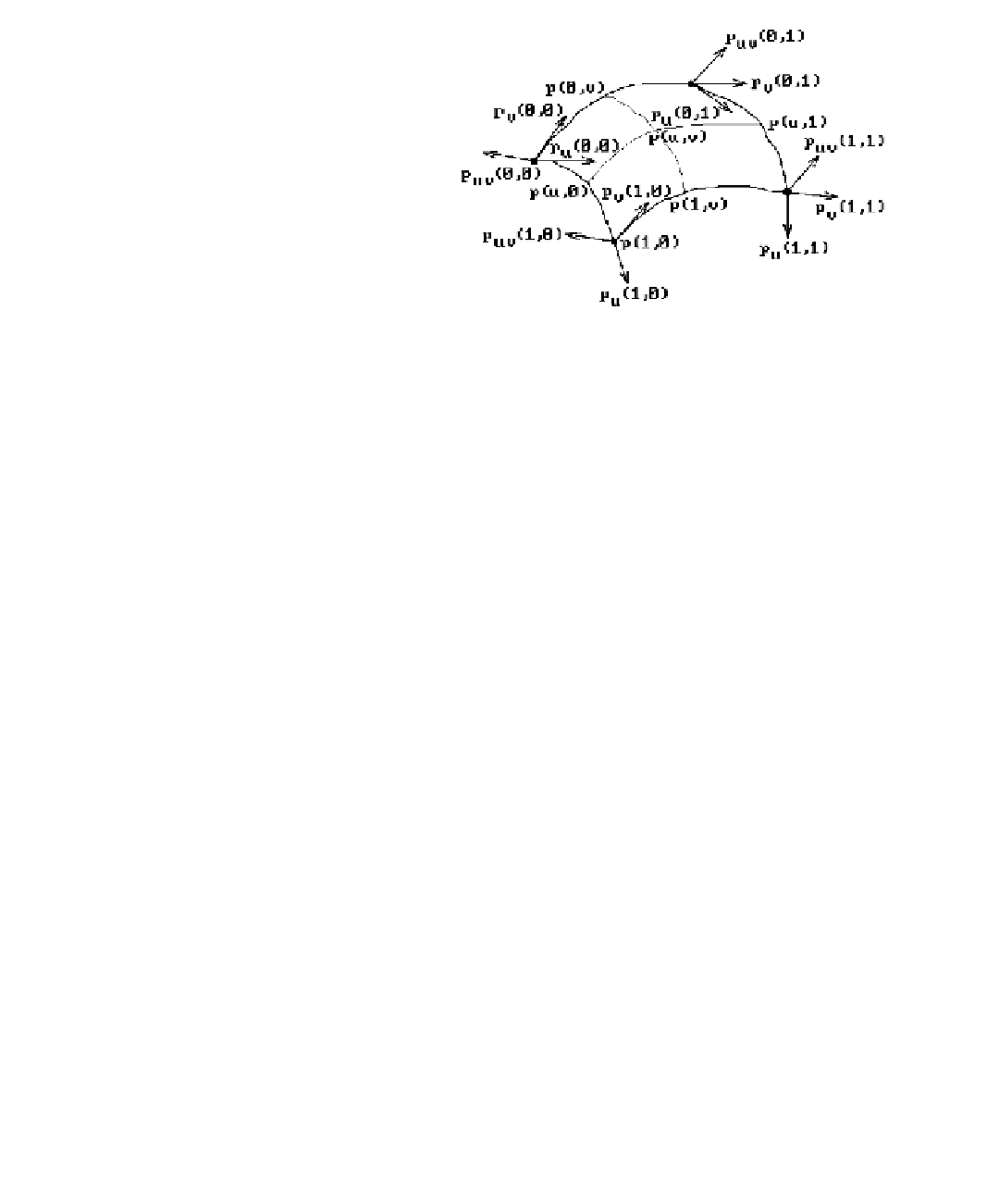
Figure 12.15.
Using the geometric
matrix to compute
p(u,v).
To find a formula for computing a point on the bicubic patch from its geometric
coefficients, one needs to take the tensor product of two cubic curves defined via their
geometric coefficients as in equation (11.37). This leads to the formula
(
)
=
UM QM
h
T
T
puv
,
V
,
(12.36a)
h
for some matrix
Q
= (
q
ij
), 0 £ i,j £ 3. By computing the points and partials of this curve
at the four points (0,0), (1,0), (0,1), and (1,1) directly from its formula, it is easy to
check that in fact the matrix
Q
is just the matrix
B
in equation (12.35) (Exercise
12.9.1). Therefore, the geometric form of the equation for the bicubic patch is
(
)
=
UM BM
h
T
T
puv
,
V
.
(12.36b)
h
This equation can also be written in the form
()
()
()
()
Fv
Fv
Fv
Fv
Ê
ˆ
1
Á
Á
Á
˜
˜
˜
2
(
)
=
(
() () () ()
)
puv
,
FuF uF uF u
B
(12.37)
1
2
3
4
3
Ë
¯
4
where the functions F
i
are defined by equations (11.14). (See equation (11.37).)
12.9.1
Example.
Consider the bicubic patch p(u,v) with geometric matrix:
(
)
(
)
(
)
(
)
0 40
, ,
-
0 22
, ,
-
022
,,
022
,,
Ê
ˆ
Á
Á
Á
˜
˜
˜
(
)
(
)
(
)
(
)
200
,,
102
,,
-
102
,,
-
102
,,
B
=
.
(
)
(
)
(
)
(
)
200
,,
100
,,
-
100
,,
-
100
,,
Ë
¯
(
)
(
)
(
)
(
)
280
,,
140
,,
--
1 40
, ,
-
1
,
-
40
,
We want to show that this patch is part of a parabolic cone.