Graphics Reference
In-Depth Information
they are developable. Recall that a surface is developable if it can be “unrolled” into
a plane. Neither the hyperboloid of one sheet nor the hyperbolic paraboloid is devel-
opable. In general, if a surface is developable, then the Gauss curvature must be zero.
See Chapter 9 in [AgoM05]. In engineering, developable and nondevelopable surfaces
are sometimes called
singly
and
doubly curved surfaces
. Developable surfaces are
desirable in manufacturing because they can be bent without stretching or tearing;
however, for a number of reasons one has to be able to deal with nondevelopable sur-
faces also and so the question arises as to how one can best flatten a nondevelopable
surface. One sample paper that addresses this issue is [YuPM00].
12.5
Sweep Surfaces
Sweep surfaces are a special case of generative models that were introduced in Section
5.3.5. They can be thought of as the envelope of the volume that we get when sweep-
ing a set (curve or volume) along a curve. In that sense, surfaces of revolution and
ruled surfaces are sweep surfaces. In this section we describe two variants that are
encountered in practice.
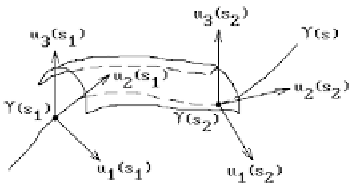
Assume that we are given
(1) a curve g : [a,b] Æ
R
3
,
(2) a coordinate system or frame (
u
1
(s),
u
2
(s),
u
3
(s)) at every point s along the curve
g(s) (the Frenet frame of the curve is a possible such coordinate system), and
(3) another curve f : [c,d] Æ
R
3
, f (t) = (f
1
(t),f
2
(t),f
3
(t)).
Define
[
]
¥
[
]
Æ
R
3
pab
:,
cd
,
(12.15a)
by
()
=
()
+
()
()
+
()
()
+
()
()
pst
,
g
s
f t
u
s
f t
u
s
f t
u
s
.
(12.15b)
1
1
2
2
3
3
See Figure 12.8.
Figure 12.8.
Sweeping a curve along a framed curve.