Graphics Reference
In-Depth Information
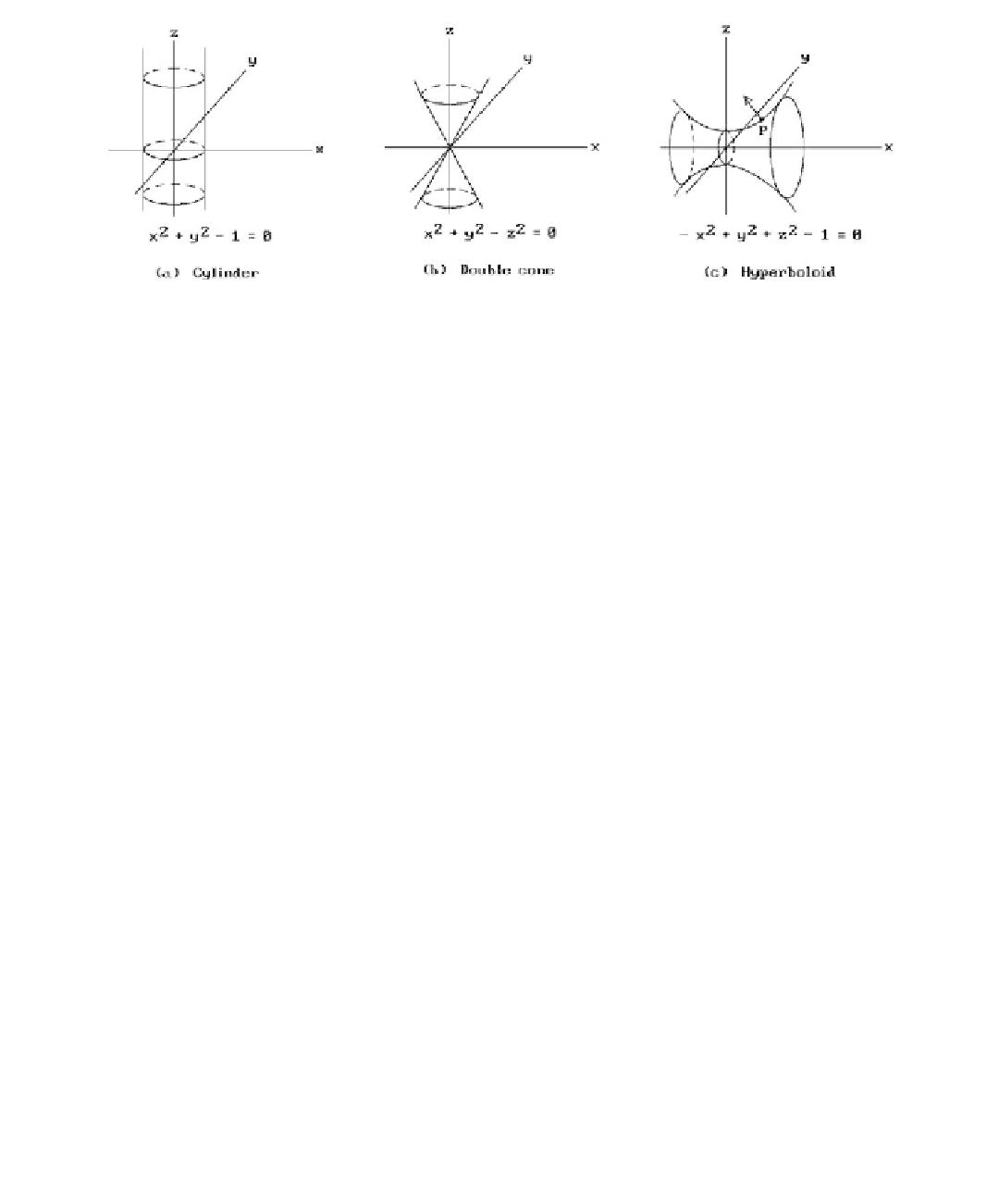
Figure 12.6.
Three quadric surfaces.
revolution (like the cyclinder, ellipsoid, paraboloid, cone, and hyperboloids) and
shows that they make good candidates for primitives in modeling systems because
one can classify their intersections.
A fundamental question for a quadric surface like for all surfaces is how one
can find a normal vector and an equation for the tangent plane at a point. Since
many of these surfaces are surfaces of revolution, we could apply the methods
developed in the last section. We could also use the fact that these surfaces can be
parameterized and tangent planes are easily computed from parameterizations.
Here, rather than using either of these two approaches, we shall describe another
powerful method. Quadric surfaces are a special case of implicit surfaces. An
implicit surface
S
in
R
3
is a surface that is the set of zeros of a function f :
R
3
Æ
R
,
that is,
{
}
3
()
=
SpR p
=Œ
f
0
.
It is a well-known fact that if
p
Œ
S
, then the gradient to f at
p
, —f(
p
), is a normal
vector to
S
at
p
(assuming that the function f is differentiable). This means that com-
puting normals for implicit surfaces is trivial. Of course, once one has the normal,
then the tangent plane is easily expressed in the point-normal form.
12.3.1
Example.
We want to find the tangent plane to the hyperboloid
S
defined
by
2
2
2
-+ + =
xyz
1
at
p
= (
3
,0,2). See Figure 12.6(c).
Solution.
Let
(
)
=-
2
2
2
fxyz
,,
x
+
y
+
z
-
1
.