Graphics Reference
In-Depth Information
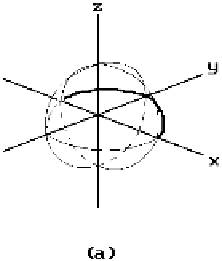
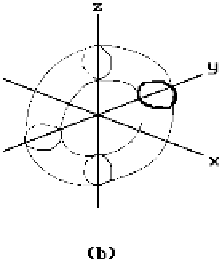
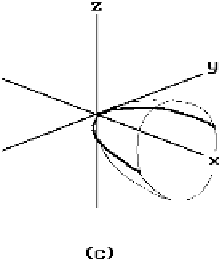
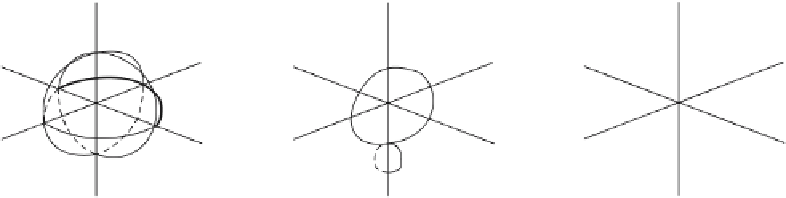
Figure 12.5.
Surfaces of revolution: sphere, torus, and paraboloid.
Æ+
(
)
+
(
)
f
Rr
u
cos
f
e
r
sin
f
u
.
q
1
q
This induces the following parameterization p(f,q) of
T
(
)
=
+
(
)
+
(
)
p
fq
,
R
u
r
cos
f
e
r
sin
f
u
q
1
q
(
(
)
(
)
)
=
r
cos ,
f
Rr
+
sin
f
cos ,
q
Rr
+
sin
f
sin
q
(12.7)
with partial derivatives
∂
∂f
p
(
)
=-
(
)
fq
,
r
sin , cos
f
r
f
cos , cos
q
r
f
sin
q
(12.8)
∂
∂q
p
(
)
=-+
(
(
)
(
)
)
fq
,
0
,
Rr
sin
f
sin ,
q
Rr
+
sin
f
cos
q
.
12.2.3 Example.
We want to find the normal vector and tangent plane to the torus
defined by equation (12.7) with r = 2 and R = 5 at
p
= (0,0,7).
Solution.
Since p(p/2,p/2) =
p
, equations (12.8) implies that
∂
∂f
p
∂
∂q
p
(
)
=-
(
)
(
)
=-
(
)
pp
22
,
200
, ,
and
pp
22 070
,
,
,
are a basis for the tangent plane. It follows that (0,0,14) = (-2,0,0) ¥ (0,-7,0) is a normal
vector and the plane has equation
(
)
∑
(
(
)
-
(
)
)
=
0014
,,
xyz
,,
007
,,
0
,
or
z -70.