Graphics Reference
In-Depth Information
hand, such as in the case of helical curves, the Frenet frames produce more intuitively
desirable results than the parallel transport planes.
Finally, Hanson and Ma ([HaMa95]) show how quaternions can be helpful in gen-
erating both Frenet and parallel transport frames.
11.14
Recursive Subdivision Curves
The discussion up to now concerned smooth curves. The splines may have had a
control polygon driving their shape, but the actual curve had a smooth parameteri-
zation. This section addresses the question of smooth curves from a different direc-
tion. We shall describe an algorithm that starts with a polygonal curve and smooths
out the curve directly by a “subdivision” process without invoking the machinery of
splines. At the end we shall still only have a polygonal curve and not actually any func-
tion that parameterizes it. The algorithm in question is the Chaikin curve subdivision
algorithm ([Chai74]). The idea behind it is to define recursively a sequence of curves
where each new curve is obtained from the previous one by “cutting off the corners.”
If we go far enough out in this sequence we shall have a smooth-looking curve. More
precisely, given a polygonal curve Chaikin introduced a new vertex in each edge that
alternately was either three quarters or one quarter of the way from the first vertex
to the second vertex of the edge. This new sequence of vertices, along with the first
and last vertex of the old curve if it was not closed, then defined the next curve. Repeat-
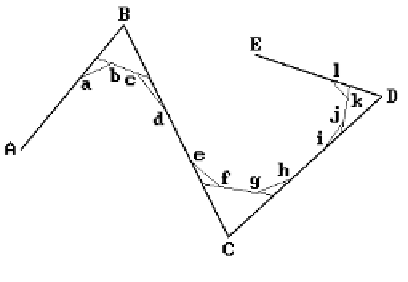
ing this process produces a convergent sequence of polygonal curves. Figure 11.41
shows two stages of this algorithm. The initial polygon is defined by the vertices
A
,
B
,
C
,
D
, and
E
. Performing the Chaikin algorithm twice produces the polygon defined
by the vertices
A
,
a
,
b
,...,
l
,
E
.
Limit curves obtained by a recursive algorithm like Chaikin's are sometimes called
recursive subdivision curves
. Riesenfeld ([Ries75]) observed that the limit curves
of the Chaikin algorithm are in fact quadratic B-splines. A good discussion of recur-
sive curve (and surface) algorithms from a historical perspective can be found in
[CavM89]. Chaikin's algorithm is a special case of much more general constructions.
Figure 11.41.
Two stages of the Chaikin
curve subdivision algorithm.