Graphics Reference
In-Depth Information
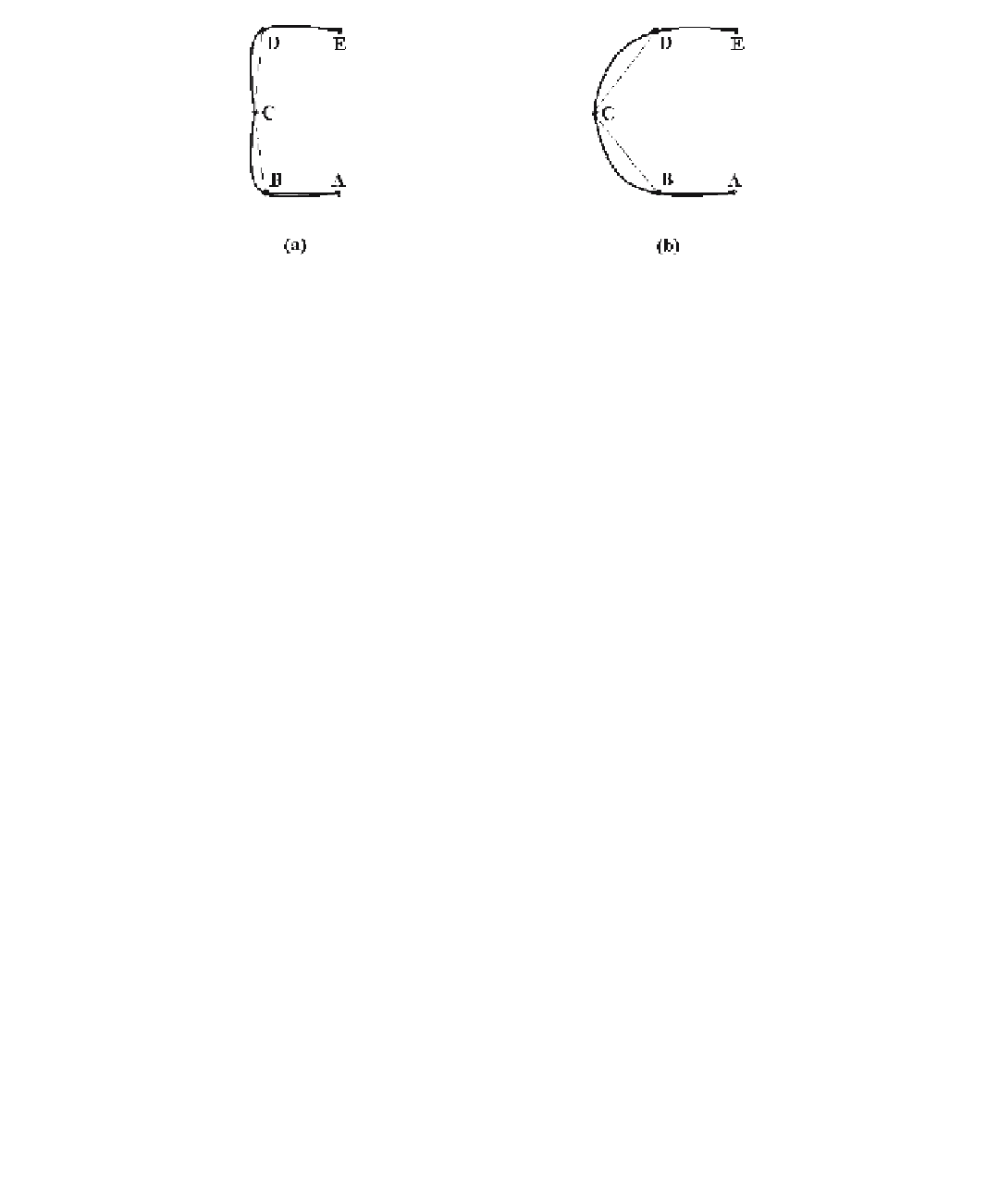
Figure 11.38.
Buckling in an interpolating spline.
Another interesting approach to analyzing the shape of cubic curves can be found
in the series of papers [Blin89a], [Blin89b], [Blin99], [Blin00a], and [Blin00b]. A
related topic has to do with buckling of interpolating spline curves or surfaces. Con-
sider Figure 11.38(a), which shows an interpolating spline through points for which
the control polygon is convex but the spline is not. The nonconvex region of the spline
near the point
C
is called a
buckle
. A similar phenomenon can happen for interpo-
lating surfaces. Buckling is usually undesirable and the hope is that moving the offend-
ing control point/s slightly would remove the flaw. Figure 11.38(b) shows a new
position for the point
C
in Figure 11.38(a) that eliminates the buckling. Note that
buckling indicates that an inflection point is present. See [VanW96] for a way to detect
buckling and remove it.
11.11
Hodographs
Although a well-established term in classical mechanics, the term “hodograph” usually
only gets mentioned in passing, if at all, in the geometric modeling literature.
Definition.
The
hodograph
of a plane curve p(u) is defined to be the subset of the
plane traced out by derivative p¢(u).
See Figure 11.39. There are some interesting applications of hodographs. See
[Forr72], [Bézi72], [SedW87], [Faro92], and [KimD93]. For example, in [Bézi72] it is
shown that the hodograph can be used to characterize geometric properties of Bézier
curves, such as inflection points and cusps. Recall from Section 11.4 that the deriva-
tive of a Bézier curve is a Bézier curve. In fact, equation (11.57) showed that if the
curve had control points
p
0
,
p
1
,...,
p
n
then the control points of the derivative are
n
a
i
, where
a
i
=
p
i+1
-
p
i
, i = 0, 1,..., n - 1. [Faro92] shows that offsets to curves whose
hodographs satisfy a certain property admit a rational parameterization. This means
that one can deal with such offsets directly without approximations. [KimD93] uses
hodographs to characterize arbitrary plane cubic curves. The answer has the same
flavor as that in [StoD89] in that the plane is divided into different regions which