Graphics Reference
In-Depth Information
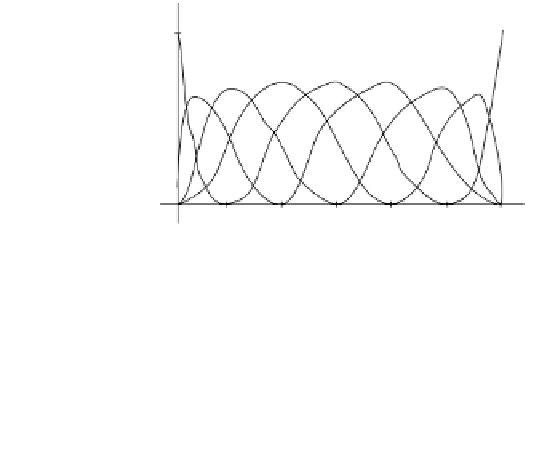
Figure 11.17.
The clamped uniform cubic
B-splines N
i,4
(u) for n
=
8.
1
N
3,4
N
4,4
N
5,4
knots = (0,0, 0,1, 2,3, 4,5, 6,6, 6,6)
()
=
(
)
NuNuj
ij
-
.
(11.73)
+
,
1
i
,
1
Using formula (11.69b) and induction on k then easily leads to
()
=
(
)
NuNuj
ijk
-
.
(11.74)
+
,
ik
,
This property of splines having the same shape is also true in the case of clamped
uniform knot vectors as long as one stays away from the ends of the knots. We saw
this in the case of linear B-splines and the hat functions. The middle three curves
N
3,4
(u), N
4,4
(u), and N
5,4
(u) in Figure 11.17 are another good example, as are the
formulas in Theorem 11.5.1.1. This then is our next goal, to analyze the N
i,k
(u) for
standard uniform knot vectors and to find formulas for the quadratic and cubic
uniform B-spline curves.
We start with the uniform quadratic B-splines and assume that u
j
= j, 0 £ j £ n +
3. Let 0 £ i £ n. It is easy to show that formulas (11.69) imply that
()
=
N
u
1
,
for i
£
u
£
i
+
1
,
and
i,
1
(11.75)
=
0
,
elsewhere
.
()
=-
(
)
( )
++-
(
)
( )
Nu uiNu i
2
uN u
(11.76)
i
,
2
i
,
1
i
+
11
,
+-
2
()
=
()
-
(
)
( )
+-
(
)
(
)
( )
+
N u
12
uiN u uii
+-
2
uN
u
i
,
3
i
,
1
i
+
11
,
( )
]
2
(
)
(
)
( )
++-
(
)
i
3
uui
--
1
Nui
3
uNu
(11.77)
i
+
11
,
i
+
21
,
Next, we want to use the N
i,3
(u) defined by (11.77) to define a quadratic B-spline curve
p(u) for control points
p
i
, i = 0,1,...,n. Before we do that and use formula (11.72)
for p(u), take a look at Figure 11.16(a) again. Over the first and last two spans there
are some “missing” B-splines. They are missing in the sense that there are
three
nonzero B-splines over the
middle
spans between 2 and n + 1, whereas there are
fewer
nonzero B-splines over those
end
spans.
Note.
There are similar missing B-splines over the end spans in the general case and
this explains why the identity in Theorem 11.5.1.4(4) fails outside of [u
k-1
,u
n+1
].