Graphics Reference
In-Depth Information
ferentiable as a spline is supposed to be. The important condition is that the splines
have finite support because that is what will give us local control. In that regard, we
should point out that the number m + 1 of spans that is supposed to contain the
support of a B-spline of degree m was not chosen in an arbitrary way. This is in general
the smallest number of spans over which an (m - 1)-differentiable piecewise polyno-
mial function is nonzero.
The proof of the next theorem is an example of how a brute force method can be
used to show that cubic splines satisfying the finite support condition exist.
11.5.1.1 Theorem.
Given distinct knots x
i-2
, x
i-1
, x
i
, x
i+1
, and x
i+2
, there is a
unique
cubic spline b
i
(t) such that
(1) b
i
(t) = 0, for t < x
i-2
or x
i+2
< t, and
(2) b
i
(x
i-1
) + b
i
(x
i
) + b
i
(x
i+1
) = 1.
Proof.
See [BaBB87]. Basically, we have four cubic polynomials, one for each span,
which gives us 16 degrees of freedom. The fact that we want the polynomials to meet
at the five knots and have the same first and second derivatives there gives us 15 con-
straints. (At the endpoints x
i-2
and x
i+2
the functions and their derivatives are zero.)
The normalizing constraint in (2) is the extra one needed for a unique solution. This
solution consists of the four polynomials
tx
-
i
-
2
()
3
16
u
,
u
=
,
x
-
x
i
-
1
i
-
2
u
tx
xx
-
-
(
)
i
-
-
1
1
()
-+ ++
3
2
16
3
uuu
3
3
1
,
=
,
i
i
i
u
tx
x
-
(
)
()
3
2
16 3
uu
-+
6
4
,
=
,
and
-
x
i
+
1
i
u
tx
-
(
)
i
+
1
()
-+
3
2
16
uuu
3
- +
3
1
,
=
,
(11.68)
x
-
x
i
+
2
i
+
1
where t ranges over the intervals [x
i-2
,x
i-1
], [x
i-1
,x
i
], [x
i
,x
i+1
], and [x
i+1
,x
i+2
], respectively.
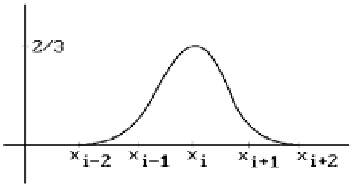
See Figure 11.13. Without condition (2), there would be many solutions.
After all these preliminaries, here are the functions we are after. We give the
Cox-de Boor recursive definition.
Figure 11.13.
A cubic B-spline basis function.