Graphics Reference
In-Depth Information
Next, assume that the ray was not parallel to the plane containing the polygon.
One needs to find the intersection of
X
with the plane containing the polygon. If such
an intersection exists, one will then have to check if it lies in the polygon. This is a
point-in-polygon type problem that we have already considered in Section 6.3, except
that now we have an arbitrary plane rather than just
R
2
. To reduce the problem to
one of two coordinates rather than three, we project the point and polygon orthogo-
nally to the xy-, xz-, or yz-plane depending on whether |n
3
|, |n
2
|, or |n
1
| is the largest,
respectively, where
n
= (n
1
,n
2
,n
3
) is a normal vector to the plane. Of course, the pro-
jection involves no work. It is simply a case of using the corresponding two coordi-
nates of the 3-coordinate points. The motivation behind making our choice of
projection depend on the largest component of
n
is numerical accuracy. We want to
have the projected polygon as large as possible and not have its vertices projected too
closely together.
10.2.2.5
Problem.
To find the intersection, if any, of the ray
X
and a convex
quadrilateral.
Solution.
This problem could be considered to be a special case of Problem 10.2.2.4
but because it is often encountered it is worth considering separately. For example,
parametric surfaces are often represented by a grid of points gotten by evaluating
their parameterization at the vertices of the subrectangles from a subdivision of their
rectangular domains. Although such surface quadrilaterals may not actually be planar
or convex, they may be assumed to be so since they will be very small. There are also
adaptive tessellation schemes that can be used to guarantee that the quadrilaterals
are within a given tolerance of being convex and planar.
The first part of the solution is the same as that in Problem 10.2.2.4. It is the test
as to whether a point in the plane belongs to a planar polygon that can be improved
in the case of a quadrilateral. We describe the solution presented in [SchS95]. It is a
generalization of Badouel's ([Bado90]) point-in-triangle solution. Assume that we are
in
R
2
. Consider a point
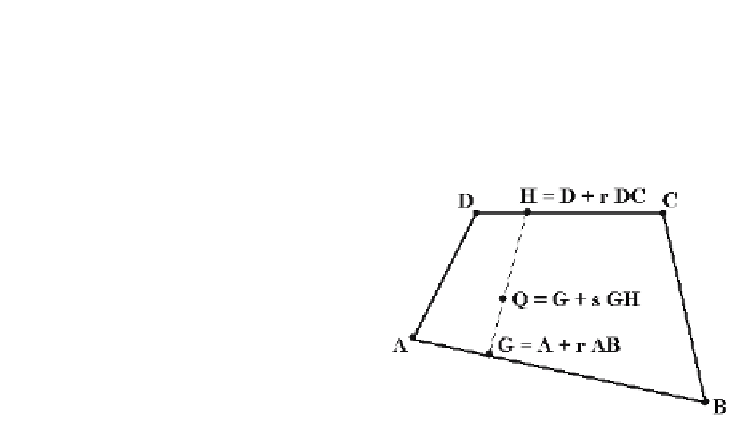
Q
and a nondegenerate convex quadrilateral with vertices
A
,
B
,
C
, and
D
. Any point of
ABCD
can be expressed in the form
GGH
+
s
,
where
GA B HDDC
=
+
r
and
=
+
r
and
0
£
r s
,
£
1
.
See Figure 10.5. Therefore, the point
Q
will belong to
ABCD
if and only if
AQ
=
r
AB
+
s
AD
+
rs
AE
,
Figure 10.5.
Surrounding test for quadrilateral.