Graphics Reference
In-Depth Information
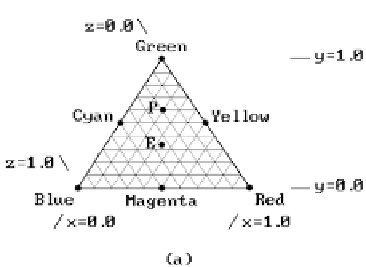
Figure 8.2.
Maxwell's triangles.
maticity diagram (the equal-sided case). This was used by Maxwell in his work on
color. The condition imposed on the selection of colors to serve as primaries is that
in equal amounts they produce white (at
E
in Figure 8.2(a)). The point
P
corresponds
to (x,y,z) = (0.2,0.6,0.2). Because the equal-sided triangle is awkward to employ
in practice, one prefers a right triangle. (We do not need z anyway.) See Figure
8.2(b).
Now it is known that not all colors can be represented as the sum of three primary
colors. What about a color that cannot be so represented? Well, we can add one of
the primary beams to this color to bring it into the range of colors we
can
represent.
This corresponds to using a negative coefficient. Although one could use negative
coefficients for the representation of colors in terms of primary colors, for practical
reasons, it was decided by the CIE to use a scheme in which negative numbers do
not
arise. Since this is
not
possible with real primaries,
imaginary primaries
were invented
(they are called that because they are not visible) called
imaginary red
,
imaginary green
,
and
imaginary blue
and denoted by
X
,
Y
, and
Z
. Then
every
color
C
can be written
as
CXYZ
=
XYZ XYZ
+
+
,
,
,
≥
0
In this way one can represent colors as triples (X,Y,Z) in a three-dimensional space
(actually its first octant). A further step is taken. Rather than using arbitrary triples
(X,Y,Z), one normalized the numbers and uses (x,y,z), where
X
XYZ
y
Y
XYZ
z
Z
XYZ
x
=
=
=
++
.
++
++
This corresponds to using the intersection of the plane X + Y + Z = 1 and the line
through the origin and (X,Y,Z). See Figure 8.3. The numbers x, y, and z are called the
chromaticity values
for
C
. Since x + y + z = 1, one only really needs x and y. Note
however that we cannot determine the original point (X,Y,Z) from just x and y. We
need some additional information and the Y value is used. In the end, therefore, the