Graphics Reference
In-Depth Information
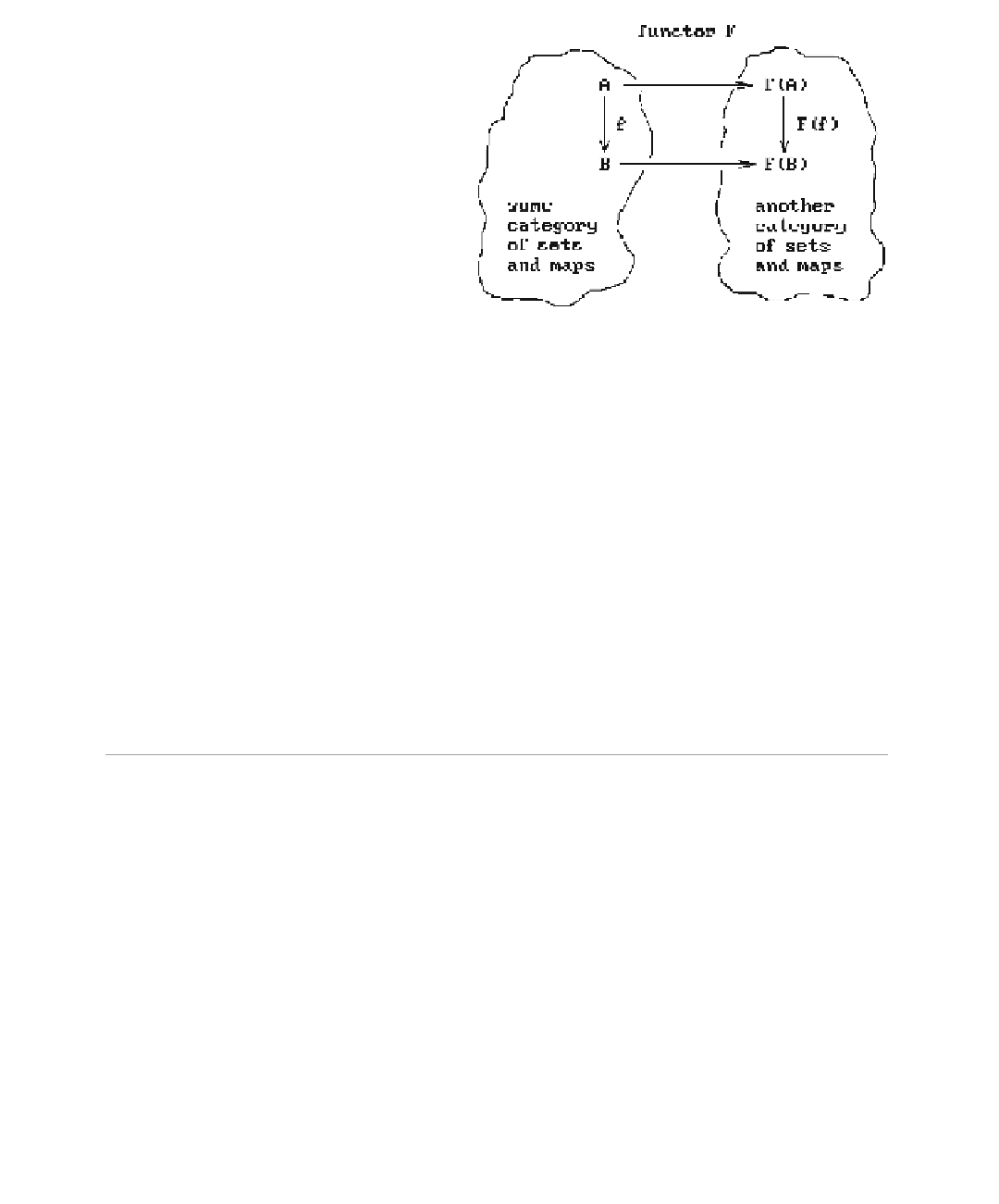
Figure 5.53.
Commutative diagrams
for representations.
for abstract concepts, representations that mimic the abstract concepts in every way.
The point of these remarks is encapsulated by Figure 5.53. Ideally, one starts with
abstract sets and transformations and then represents them by other sets and trans-
formation in such a way that everything is preserved, meaning that one gets com-
mutative diagrams. In the context of geometric modeling, there are objects,
transformations of objects, and functions on these objects. Representations act on
maps as well as sets and need to produce commutative diagrams. It would be nice if
representations were what are called
functors
between
categories
but they are not.
(The terms “functor” and “category” have a very definite meaning in mathematics.
They help make precise the notion of commutative diagrams that we talk about at
various places in this topic, but that is another story that we cannot go into here.)
Nevertheless it is worth reminding the reader of what one should at least strive for,
or at least keep in mind, even if it is not possible to achieve in practice. Recall our
discussion in Section 5.7 and Figure 5.35.
5.13
E
XERCISES
Section 5.2
Explain why the unit square [0,1] ¥ [0,1] is
not
an r-set in
R
3
.
5.2.1
5.2.2
Prove that r(r
X
) = r
X
.
5.2.3
Give an intuitive but convincing argument for why the regularized set operators take r-
sets to r-sets.
Section 5.3.3
5.3.3.1
Here is a slight variation of the usual linear polyhedron.
Definition.
A set
X
Õ
R
n
that can be obtained from a given collection of open linear
halfplanes by a finite sequence of set operations consisting of the complement and
intersection operator is called a
Nef polyhedron
.