Graphics Reference
In-Depth Information
Another issue when it comes to faces is how to represent them? We shall see in
Section 5.9 that to represent a face
F
we can
(1) represent the halfspace in whose boundary the face
F
lies (for example, in the
case of a cylinder, use its equation),
(2) represent the boundary edges of
F
(the boundary of a face is a list of edges),
and
(3) maintain some neighborhood information for these bounding edges and
orient the edges (for example, we can arrange it so that the inside of the face
is to the right of the edge or we can store appropriate normal vectors for the
edges).
This scheme works pretty well for simple surfaces but for more complicated surfaces
one needs more.
5.3.4
Euler Operations
Representation schemes based on using Euler operations to build objects are an
attempt to have a boundary representation meet at least part of the validity issue head
on. The idea is to permit only boundary representations that have a valid Euler char-
acteristic. If we only allow operations that preserve the Euler characteristic or that
change it in a well-defined way (such operations are called
Euler operations
), then we
achieve this. Of course this is only a part of what is involved for an object not to be
a nonsense object. Nevertheless we have at least preserved the combinatorial validity
since the Euler characteristic is a basic invariant of combinatorial topology. As for
metric validity, one still must do a careful analysis of face/face intersections. In any
case, to say that a modeler is built on Euler operations means that it represents objects
as a sequence of Euler operations.
Topologically, Euler operations are based on elementary collapses and expansions
and/or cutting and pasting (see Sections 7.2.4 and 6.4 in [AgoM05], respectively).
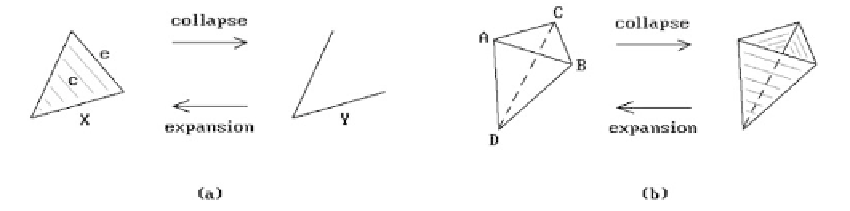
Figure 5.13 shows two elementary collapse and expansion examples. One says that
the space
Y
consisting of the two segments on the right of Figure 5.13(a) is obtained
from the solid triangle
X
on the left via an elementary collapse of the cell
c
from the
edge
e
. Conversely, the space
X
is said to be obtained from
Y
via an elementary expan-
sion. Figure 5.13(b) shows another elementary collapse and expansion, this time
involving a three-dimensional cell
ABCD
and a face
ABC
. Figure 5.14 shows a cutting
Figure 5.13.
Elementary collapses/expansions.