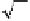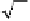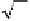Graphics Reference
In-Depth Information
6
7
1
7
23
7
Ê
ˆ
-
Á
Á
Á
Á
Á
˜
˜
˜
˜
˜
1
7
6
7
23
7
M
12
=
.
23
7
23
7
5
7
-
Ë
¯
We can also see from the expression for
q
1/2
and equation (4.26) that M
1/2
defines a
rotation about the directed line through the origin with direction vector (1,1,0) and
angle 2a, where
3
14
cos
a=2
.
It is clear that the quaternions
c
(t) defined by Lemma 4.14.1 do indeed lie on a
great circles in the unit sphere of the quaternions. We have solved the uniform spacing
problem, but unfortunately this is not the end of the story as far as animation is con-
cerned. Two points on a circle divide the circle into two arcs. If the points are not
antipodal points, then one typically is interested in the smaller arc. In our situation
we cannot simply always take the smaller arc without further consideration because
we are representing rotations by quaternions, and if
q
is a unit quaternion, both
q
and -
q
correspond to the same rotation in
SO
(3). The solution suggested in [WatW92]
is, given representations
a
and
b
for two rotations, to choose between
a
,
b
and
a
, -
b
.
One compares the distance between
a
and
b
, |
a
-
b
|, to the distance between
a
and
-
b
, |
a
+
b
|. If the former is smaller use
a
,
b
otherwise use
a
, -
b
.
After getting our uniformly spaced quaternions
c
(t
i
) along the arc, if we were to
do a linear interpolation between them, then the motion may look jerky. It is better
to smooth things out by using Bezier curves or, more generally, splines, but this is
somewhat more complicated in quaternion space than it was in
R
n
. See [BCGH92],
[WatW92], [Hogg92], or [Shoe93] for what needs to be done.
4.15
Conclusions
Transformations were at the center of all the discussions in this chapter. We would
like to emphasize one last time that when it comes to representing and defining affine
transformations one should do that via frames if at all possible. Frames are ortho-
normal basis and these are easy to define. Without them, geometric modeling for n-
dimensional objects would become very complicated when n is larger than 2. Once
one has a frame it can be interpreted as a transformation, a coordinate system, or as
defining a change of coordinates. See Chapter 2 in [AgoM05] for more details.
The main role of homogeneous coordinates and projective space is as the natural
setting for projective transformations. The mathematics becomes much easier. A prac-
tical application is that one can replace all transformations, including translations,
with matrices in uniform way. We described some of the main perspective and par-
allel projections.