Graphics Reference
In-Depth Information
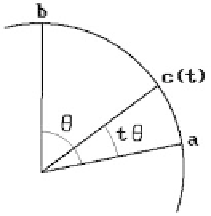
Figure 4.26.
Interpolating between two quaternions.
then M
q
Œ
SO
(3) and the map of
R
3
that sends
p
to
p
M
q
is a rotation R
q
about the
line through the origin with direction vector
n
through the angle 2q. This mapping
3
unit quaternions
Æ
Æ
rotations of
R
about the origin
q
R
q
has the property that R
q
= R
-
q
.
Now, suppose an object is moved by a one-parameter family of matrices M(s) Œ
SO
(3). Assume that we have only specified this family at a fixed set of values s
i
. How
can we interpolate between these values? In animation such an interpolation is called
in-betweening
. A simple interpolation of the form
()
+-
(
)
(
)
tM s
1
t M s
i
i
+
1
would not work because the interpolants would not again be elements of
SO
(3). One
could try to use Euler angles, but there are problems with this also. See [Shoe85]. A
better way is to translate our maps into quaternions and to look for a one-parameter
family of unit quaternions q(s) that interpolates between two quaternions
a
and
b
.
However, a simple linear interpolation followed by a normalization to get unit quater-
nions does not work well either for the same reason that one does not get a uniform
subdivision of an arc of a circle by centrally projecting a uniform subdivision of the
chord connecting its endpoints. What would happen in the animation is that the object
would move faster in the middle of the interpolation. A better solution is to subdivide
the arc of the great circle in
S
3
connecting
a
and
b
. See Figure 4.26.
4.14.1 Lemma.
Let
a
and
b
be two unit quaternions that make an angle of qπ0
with each other, that is,
a
·
b
= cos q and 0 <q<p. Then the unit quaternion
c
(t) that
lies in the plane spanned by
a
and
b
and which makes an angle tq with
a
, 0 £ t £ 1 is
defined by the equation
(
)
sin
sin
1
-
t
q
sin
sin
t
q
q
()
=
c
t
a
+
b
.
(4.28)
q
Proof.
By hypothesis,
()
=+
c
tr s
a
b