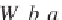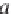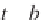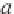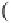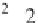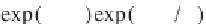Geoscience Reference
In-Depth Information
where
b
denotes the position (translation) and
a
(>0) the scale (dilation) of
the wavelet (Lau and Weng 1995). h e wavelet transform of the signal
y
(
t
)
about the mother wavelet ˈ(
t
) is dei ned as the convolution integral
where ˈ* is the complex conjugate of ˈ. h ere are many mother wavelets
available in the literature, such as the classic
Haar
wavelet, the
Morlet
wavelet,
or the
Daubechies
wavelet. h e most popular wavelet in geosciences is the
Morlet wavelet introduced by French geophysicist Jean Morlet (1931-2007),
which is dei ned by
where ʷ is the time and ˉ
0
is the wave number (Torrence and Compo
1998). h e wave number is the number of oscillations within the wavelet
itself. We can easily compute a discrete version of the Morlet wavelet
wave
by translating the above equation into MATLAB code, where
eta
is the non-
dimensional time and
w0
is the wave number. Changing
w0
produces wavelets
with dif erent wave numbers. Note that it is important not to use
i
for index
in
for
loops, since it is used here for imaginary unit (Fig. 5.15).
clear
eta = -10 : 0.1 : 10;
w0 = 6;
wave = pi.^(-1/4) .* exp(i*w0*eta) .* exp(-eta.^2/2);
plot(eta,wave)
xlabel('Position')
ylabel('Scale')
title('Morlet Mother Wavelet')
In order to familiarize ourselves with wavelet power spectra, we use a pure
sine wave with a period i ve and additive Gaussian noise.
clear
rng(0)
t = 0 : 0.5 : 50;
x = sin(2*pi*t/5) + randn(size(t));
As a i rst step, we need to dei ne the mother wavelet and its wave number
w0
.
mother = 'morl';
w0 = 6;