Graphics Reference
In-Depth Information
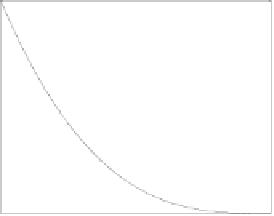
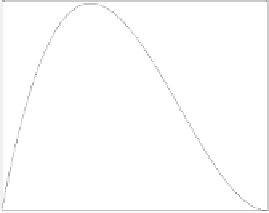
Figure 1.1 shows the behavior of the basis functions for different values of the
parameter
t
∈
[0
,
1], for cubic Bezier-Bernstein polynomial.
1
0.45
0.9
0.4
0.8
0.35
0.7
0.3
0.6
0.25
0.5
0.2
0.4
0.15
0.3
0.1
0.2
0.05
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t
t
(a)
(b)
1
0.45
0.9
0.4
0.8
0.35
0.7
0.3
0.6
0.25
0.5
0.2
0.4
0.15
0.3
0.1
0.2
0.05
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
t
t
(c)
(d)
Fig. 1.1.
Behavior of the basis functions for cubic B-B curve.
Consider the equation of a Bezier curve in a matrix form for compact
representation. For a cubic curve, we have
⎛
⎝
⎞
⎠
V
0
V
1
V
2
V
3
P
(
t
)=
(1
t
)
t
3
t
)
3
3
t
(1
t
)
2
3
t
2
(1
−
−
−
.
(1.20)
This can be written as
⎛
⎝
⎞
⎠
⎛
⎝
⎞
⎠
−
−
V
0
V
1
V
2
V
3
13
31
P
(
t
)=
t
3
t
2
t
1
−
3
630
−
33 00
1000
(1.21)
=
T
C
V
.
Cohen and Risenfeld [42] have generalized this representation to
P
(
t
)=
T
C
V


















































































Search WWH ::

Custom Search