Snakes and Active Contours - Bezier and Splines in Image Processing and Machine Vision - page 188

9.5 Minimizing the Snake Energy Using Dynamic
Programming

One of the most popular methods today is the dynamic programming ap-
proach as implemented by the Viterbi algorithm [167] as proposed by Amini,
Weymouth, and Jain [3] and extended by Geiger et al. [66]. The approach
of dynamic programming is to solve the optimization problem by studying a
collection, or family, of problems where the particular problem in question is
a member. This concept is known as embedding .
The Viterbi method is closely related to Dijkstra's algortithm [59], which
solves for the shortest path in a network between two points by finding the
shortest paths to all points. The major difference is that the Viterbi algorithm
calculates the shortest path on a trellis , whereas Dijkstra's algorithm finds the
shortest path in a network. Returning to the snake minimization problem at
hand, instead of attempting to find the local minimum directly, the Viterbi
algorithm eciently evaluates a very large set of alternative solutions in the
neighborhood of the current best solution and then picks the minimum. The
process is repeated until convergence is attained.
The dynamic programming formulation of snakes requires the snake to be
discretized to a finite set of points in the image pixel domain as before. To limit
the number of possible solutions examined, the position of each control point
on the snake on the next iteration is constrained to a finite set of positions,
x i ∈ X i , where each set X i contains m positions. With the snake discretized

and the domain of possible solutions constrained in this manner, the set of
all possibilities for the next configuration of the snake can be visualized as a
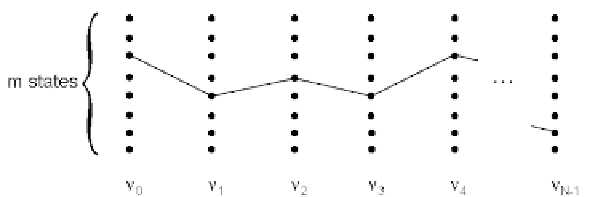
trellis as illustrated in Figure 9.6.

Fig. 9.6. Snake configuration space visualized as a trellis.

It is possible, but not at all practical, to exhaustively enumerate all possi-
ble configurations to determine the snake with minimum energy. This would
require O( m N ) evaluations of the energy function, where m is the number of
candidate positions and N is the number of control points forming the snake.
This is prohibitively expensive for even small values of m and N . For example,
if m = N = 30, this task would require 30 30 =2

×

10 44 evaluations. Assuming