Geometric Tests - 3D Math Primer for Graphics and Game Development - page 728

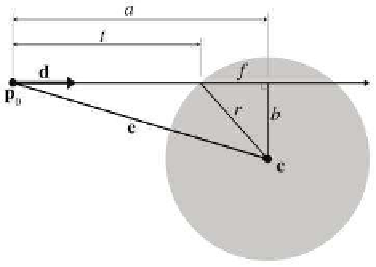
Figure A.8
Intersection of a ray and sphere

Now we project e onto d (see Section 2.11.2). The length of this vector is
a, and can be computed by

a = e d .
Now all that remains is to compute f. First, by the Pythagorean theo-
rem, we clearly see that

f 2 + b 2 = r 2 .
We can solve for b 2 by using the Pythagorean theorem on the larger triangle:

a 2 + b 2 = e 2 ,
b 2 = e 2 − a 2 ,

where e is the distance from the origin of the ray to the center, that is, the
length of the vector e . Thus, e 2 can be computed by

e 2 = e e .

Substituting and solving for f, we get

f 2 + b 2 = r 2 ,
f 2 + (e 2 − a 2 ) = r 2 ,
f 2 = r 2 − e 2 + a 2 ,

r 2 − e 2 + a 2 .

f =

Finally, solving for t, we have

t = a − f

Parametric intersection
of a ray and a circle or
sphere

= a − r 2 − e 2 + a 2 .

If the argument to the square root (r 2 − e 2 + a 2 ) is negative, then the
ray does not intersect the sphere.