Curves in 3D - 3D Math Primer for Graphics and Game Development - page 712

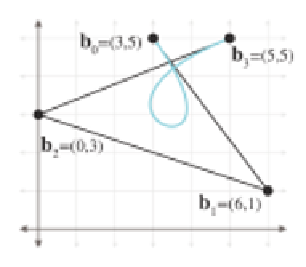
3. Consider the Bezier curve in the figure below.
(a) Use de Casteljau to determine the position on the curve at t = 0.40.
(b) Convert the curve to Hermite form.
(c) Convert the curve to monomial form.
(d) Check your work on part (a) by substituting t = 0.40 into the poly-
nomial computed in part (c).
(e) What is the velocity polynomial function v(t)?
(f) What is the velocity at t = 0.40, t = 0.00, and t = 1.00?
4. Prove that the quadratic Bernstein basis polynomials sum to 1 for any value
of t.
5. Where should we put the Bezier control points to get a “constant curve”
where p(t) always returns the same point?
6. Where should we put the Bezier control points to get a linear “curve,”
which is a straight line segment with constant velocity?
7. Where should we put the Bezier control points to get a straight line shape,
but this time the velocity of the curve follows the smoothstep pattern: it
starts at zero, accelerates to a maximum velocity at the middle, and then
decelerates to end with zero velocity?
8. Describe the motion of a particle that moves along the Bezier curve where
b 0 = b 2 and b 1 = b 3 .
9. Consider the projectile herring sandwich from Exercise 2. Assume you
need to animate this sandwich, and the only tools available to you are
cubic Bezier curves. Where should you put the four Bezier control points
to get physically realistic motion, which is quadratic? Don't worry about
the total duration the sandwich is airborne; consider only the shape of the
trajectory.
10. To plot the shape of the parabola in Figure 12.8 (page 588), the authors
tabulated a list of x, y image-space coordinates of the center of the mass of
the board, and then did a least-squares fit to arrive at the equation for the
parabola y = −0.364x 2 +1.145x+2.110. The pen tool in Adobe Illustrator,