Mechanics 1: Linear Kinematics and Calculus - 3D Math Primer for Graphics and Game Development - page 543

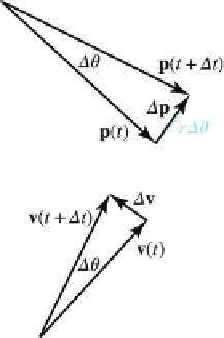
On the left side of Figure 11.14 we see a particle moving in uniform
circular motion during a finite time step ∆t. The figure examines the state
of the particle at time t and also at a later time t + ∆t.
Let's consider instantaneous velocity and acceleration, starting with
a geometric tack. Examine the triangles on the right-hand side of Fig-
ure 11.14. The triangle on the top shows the change in position over some
time interval ∆t, as a result of the angular change ∆θ. It is an isosceles
triangle in which the legs have length r, the radius of the circle, and the
base is ∆ p , which is the net change in position during the interval. The
bottom triangle depicts the change in velocity over this same interval, and
it is also an isosceles triangle. The legs of the bottom triangle have length
s, since we are hypothesizing that the velocity has constant magnitude,
and the base is ∆ v . The two triangles are similar, since both triangles are
isosceles with the included angle ∆θ, so we can write

∆ v
s

∆ p
r

= .

In general, the length of ∆ p measures a “shortcut” through the circle,
rather than the actual distance traveled around the perimeter of the circle,
which is r∆θ = s∆t. But consider what happens as ∆t and ∆θ become
very small, as shown in Figure 11.15.

Figure 11.15
A small rotation.

Notice that as ∆θ grows smaller and smaller, the length of ∆ p ap-
proaches the true distance, and in the limit, the two distances are equal:

lim
∆t→0

∆ p = s∆t.