Geometric Primitives - 3D Math Primer for Graphics and Game Development - page 335

As we mentioned, degenerate cases can make even these relatively clear-
cut definitions blurry. For example, what about a polygon with two con-
secutive coincident vertices, or an edge that doubles back on itself? Are
those polygons considered convex? In practice, the following “definitions”
for convexity are often used:

• If my code, which is supposed to work only for convex polygons, can

deal with it, then it's convex. (This is the “if it ain't broke, don't fix
it” definition.)

• If my algorithm that tests for convexity decides it's convex, then it's

convex. (This is an “algorithm as definition” explanation.)

For now, let's ignore the pathological cases, and give some examples of
polygons that we can all agree are definitely convex or definitely concave.
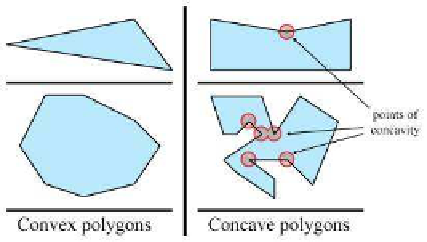
The top concave polygon in Figure 9.28 has one point of concavity. The
bottom concave polygon has five points of concavity.

Figure 9.28
Convex vs. concave
polygons

Any concave polygon may be divided into convex pieces. The ba-
sic idea is to locate the points of concavity (called “reflex vertices”) and
systematically remove them by adding diagonals. O'Rourke [52] provides
an algorithm that works for simple polygons, and de Berg et al. [12] show
a more complicated method that works for complex polygons as well.
How can we know if a polygon is convex or concave? One method
is to examine the sum of the angles at the vertices. Consider a convex
polygon with n vertices. The sum of interior angles in a convex polygon is
(n − 2)180 o . We have two different ways to show this to be true.
First, let θ i measure the interior angle at vertex i. Clearly, if the polygon
is convex, then θ i ≤ 180 o . The amount of “turn” that occurs at each

vertex will be 180 o − θ i . A closed polygon will of course turn one complete