Game Development Reference
In-Depth Information
There is one slight problem with this: the magnitude of the cross prod-
uct is not sensitive to the ordering of the vertices—magnitude is by defini-
tion always positive. This will not work for points outside the triangle, since
these points must always have at least one negative barycentric coordinate.
Let's see if we can find a way to work around this problem. It seems like
what we really need is a way to calculate the length of the cross product
vector that would yield a negative value if the vertices were enumerated in
the “incorrect” order. As it turns out, there is a very simple way to do this
with the dot product.
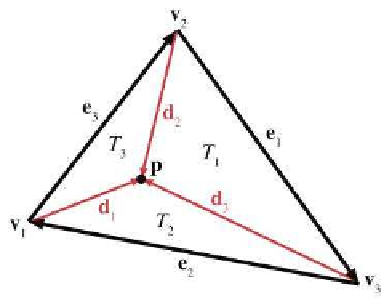
Let's assign
c
to be the cross product of two edge vectors of a triangle.
Remember that the magnitude of
c
will equal twice the area of the triangle.
Assume we have a normal
n
of unit length. Now,
n
and
c
are parallel, since
they are both perpendicular to the plane containing the triangle. However,
they may point in opposite directions. Recall from Section 2.11.2 that the
dot product of two vectors is equal to the product of their magnitudes times
the cosine of the angle between them. Since we know that
n
is a unit vector,
and the vectors are either pointing in the exact same or the exact opposite
direction, we have
c
n
=
c
n
cosθ
=
c
(1)(±1)
= ±
c
.
Dividing this result by two, we have a way to compute the “signed area” of
a triangle in 3D. Armed with this trick, we can now apply the observation
from the previous section, that each barycentric coordinate b
i
is propor-
tional to the area of the subtriangle T
i
. Let us first label all of the vectors
involved, as shown in Figure 9.21.
Figure 9.21
Computing barycentric
coordinates in 3D








Search WWH ::

Custom Search