Geometric Primitives - 3D Math Primer for Graphics and Game Development - page 319

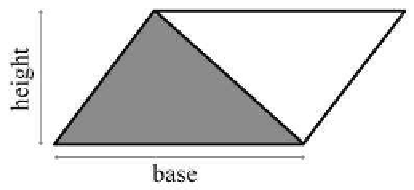
Figure 9.16
A triangle enclosed in a
parallelogram

If the altitude is not known, then Heron's formula can be used, which re-
quires only the lengths of the three sides. Let s equal one half the perimeter
(also known as the semiperimeter). Then the area is given by

Heron's formula for the
area of a triangle

s = l 1 + l 2 + l 3
2

= p

2 ,

A = s(s − l 1 )(s − l 2 )(s − l 3 ).

Heron's formula is particularly interesting because of the ease with which
it can be applied in 3D.

Often the altitude or lengths of
the sides are not readily available
and all we have are the Cartesian
coordinates of the vertices. (Of
course, we could always compute
the side lengths from the coordi-
nates, but there are situations for
which we wish to avoid this rela-
tively costly computation.) Let's see
if we can compute the area of a
triangle from the vertex coordinates
alone.
Let's first tackle this problem in
2D. The basic idea is to compute, for
each of the three edges of the trian-
gle, the signed area of the trapezoid
bounded above by the edge and below by the x-axis, as shown in Fig-
ure 9.17. By “signed area,” we mean that the area is positive if the edge
points from left to right, and negative if the edge points from right to left.
Notice that no matter how the triangle is oriented, there will always be at
least one positive edge and at least one negative edge. A vertical edge will

Figure 9.17
The area “beneath” an edge vector