Geometric Primitives - 3D Math Primer for Graphics and Game Development - page 301

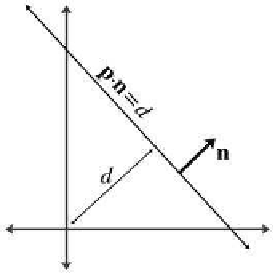
If we assign the vector n = [a,b], we can write Equation (9.3) using
vector notation as

Implicit definition of
infinite 2D line using
vector notation

p n = d. (9.4)

Since this form has three degrees of free-
dom, and we said that an infinite line in
2D has only two, we know there is some
redundancy. Note that we can multiply
both sides of the equation by any con-
stant; by so doing, we are free to choose
the length of n without loss of general-
ity. It is often convenient for n to be a
unit vector. This gives n and d interest-
ing geometric interpretations, as shown
in Figure 9.6.
The vector n is the unit vector or-
thogonal to the line, and d gives the
signed distance from the origin to the
line. This distance is measured perpen-
dicular to the line (parallel to n ). By
signed distance, we mean that d is pos-
itive if the line is on the same side of the origin as the normal points. As
d increases, the line moves in the direction of n . At least, this is the case
when we put d on the right side of the equals sign, as in Equation (9.4). If
we move d to the left side of the equals sign and put zero on the right side,
as in the traditional form, then the sign of d is flipped and these statements
are reversed.
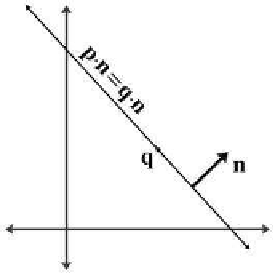
Notice that n describes the “orientation” of the line, while d describes
its position. Another way to describe the position of the line is to give a
point q that is on the line. Of course there are infinitely many points on
the line, so any point will do (see Figure 9.7).

Figure 9.6
Defining a line using a perpendicular
vector and distance to the origin

Figure 9.7
Defining a line using a perpendicular vector
and a point on the line