Geometric Primitives - 3D Math Primer for Graphics and Game Development - page 296

the circle, ellipse, parabola, and hyperbola, all of which can be described
in the standard implicit form Ax 2 + Bxy + Cy 2 + D = 0.
Metaballs [7] is an implicit method for representing fluid and organic
shapes. The volume is defined by a collection of fuzzy “balls.” Each ball
defines a three-dimensional scalar density function based on the distance
from the center of the ball, with zero distance being the maximal value and
greater distances having lower values. We can define an aggregate density
function for any arbitrary point in space by taking the sum of the density
of all the balls at that point. The twist with metaballs is that the volume
of the fluid or organic object is defined to be the region where the density
exceeds some nonzero threshold. In other words, the balls have a “fuzzy”
region around them that extends outside of the volume when the ball is in
isolation. When two or more balls come together, the fuzzy regions interfere
constructively, causing a graceful “bond” of solid volume to materialize in
the region in between the balls, where no such solid would exist if either ball
were in isolation. The marching cubes algorithm [43] is a classic technique
for converting an arbitrary implicit form into a surface description (such as
a polygon mesh).
Another general strategy for describing shapes is the parametric form.
Once again, the primitive is defined by a function, but instead of the spatial
coordinates being the input to the function, they are the output. Let's begin
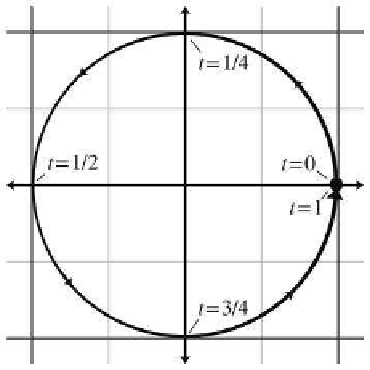
with a simple 2D example. We define the following two functions of t:

Unit circle in parametric
form

x(t) = cos 2πt, y(t) = sin 2πt.

The argument t is known as the parameter and is independent of the coor-
dinate system used. As t varies from 0 to 1, the point (x(t),y(t)) traces out

Figure 9.1
Parametric circle