Introduction to Matrices - 3D Math Primer for Graphics and Game Development - page 129

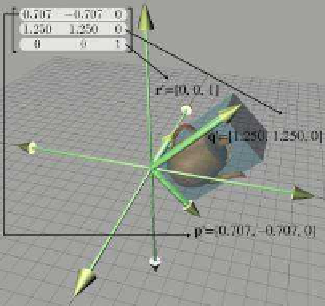
Now consider the 3D transformation matrix
2 3

0.707 −0.707 0

4 5

1.250 1.250 0 .

0 0 1

Extracting the basis vectors from the rows of the matrix, we can visual-
ize the transformation represented by this matrix. The transformed basis
vectors, cube, and teapot are shown in Figure 4.5.

Figure 4.5
Teapot, unit cube, and basis vectors after
transformation

As we can see, the transformation consists of a clockwise rotation of
45 o about the z-axis as well as a nonuniform scale that makes the teapot
“taller” than it was originally. Notice that the +z basis vector is unaltered
by the transformation, because the third row of the matrix is [0,0,1].
By interpreting the rows of a matrix as basis vectors, we have a tool
for deconstructing a matrix. But we also have a tool for constructing one!
Given a desired transformation (i.e., rotation, scale, and so on), we can
derive a matrix that represents that transformation. All we have to do
is figure out what the transformation does to the basis vectors, and then
place those transformed basis vectors into the rows of a matrix. We use
this tool repeatedly in Chapter 5 to derive the matrices to perform basic
linear transformations such as rotation, scale, shear, and reflection.
The bottom line about transformation matrices is this: there's nothing
especially magical about matrices. Once we understand that coordinates
are best understood as coe cients in a linear combination of the basis
vectors (see Section 3.3.3), we really know all the math we need to know to
do transformations. So from one perspective, matrices are just a compact
way to write things down. A slightly less obvious but much more compelling
reason to cast transformations in matrix notation is to take advantage of
the large general-purpose toolset from linear algebra. For example, we can