Introduction to Matrices - 3D Math Primer for Graphics and Game Development - page 127

What sort of transformation does this matrix represent? First, let's extract
the basis vectors p and q from the rows of the matrix:

p = 2 1 ;

q = −1 2 .

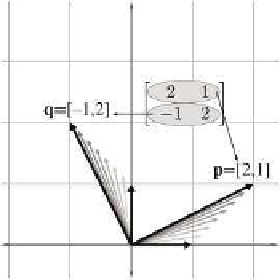
Figure 4.1 shows these vectors in the Cartesian plane, along with the “orig-
inal” basis vectors (the x-axis and y-axis), for reference.

As Figure 4.1 illustrates, the +x ba-
sis vector is transformed into the vector
labeled p above, and the y basis vector
is transformed into the vector labeled
q . So one way to visualize a matrix in
2D is to visualize the L shape formed
by the row vectors. In this example,
we can easily see that part of the trans-
formation represented by matrix M is
a counterclockwise rotation of approxi-
mately 26.5 o .
Of course, all vectors are affected
by a linear transformation, not just the
basis vectors. We can get a very good
idea what this transformation looks like
from the L, and we can gain further in-
sight on the effect the transformation
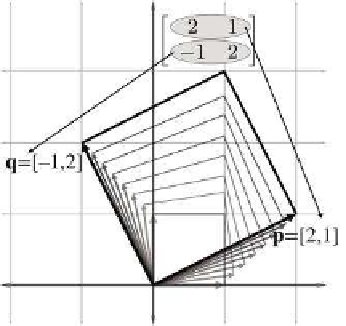
has on the rest of the vectors by completing the 2D parallelogram formed
by the basis vectors, as shown in Figure 4.2.

Figure 4.1
Visualizing the row vectors of a 2D
transform matrix

Figure 4.2
The 2D parallelogram formed by the
rows of a matrix