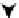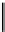Biomedical Engineering Reference
In-Depth Information
Prior Knowledge
p(
q
)
True State
of the World
q
p(d |
q
)
Bayes'
rule
Posterior
p(
q
| d)
Sensory Data
d
Estimate
q
of
q
^
Fig. 4.1
Bayesian statistical models. In the Bayesian scheme, the observer gathers data from the
outside world which is modelled based on parameters represented by
θ
. The data,
d
, is combined
with prior knowledge on the parameters,
θ
, to infer a posterior probability distribution for the
parameters using Bayes' rule [Eq. (
4.1
)]. This in turn allows to determine an estimate for the model
parameters
p
(
d
|
θ
). The main function on which decisions are based is the posterior distribution
p
(
θ
|
d
) which gives the conditional probability of the model parameter
θ
given the
observed data
d
. To calculate this posterior distribution, we use Bayes' rule
pd
pd p
pd
(|)()
()
qq
(|)
q
=
,
(4.1)
where
p
(
d
|
θ
) is the conditional probability of the data given the model parameter,
θ
(Fig.
4.1
).
In the ield of statistics, the probability distribution
p
(
d
|
θ
) is also called a genera-
tive model since it maps outside stimuli into sensory neural responses (in our context).
The probability distribution of the model parameter
θ
,
p
(
θ
), is the prior distribution
that is related to properties of the outside world. The experimenter will often be able
to manipulate these priors. The distribution of responses irrespective of the stimuli (or
of the current state of the world) is called the marginal distribution,
p
(
d
). This mar-
ginal distribution normalizes Eq. (
4.1
) such that the integral of the posterior distribu-
tion over
θ
is unity. When we ix the data
d
and let
θ
vary, the generative model
p
(
d
|
θ
)
becomes what is known as the likelihood function in statistics. One conventional
method of estimating
θ
consists in selecting the value,
q
, that maximizes the likeli-
hood given the data. This decision rule is called “maximum likelihood”. The analo-
gous principle in the Bayesian case consists in selecting the maximum of the posterior
distribution, or “maximum a posteriori” (MAP) estimate. Alternatively, another valid
rule consists in computing the mean of the posterior distribution. The use of these
decision rules will be illustrated in the following sections.
Often, knowing
p
(
d
) is not necessary as we only need to know the dependence of
the posterior on the model parameter, and
p
(
d
) only acts as a normalizing constant.
This is exploited by computing the product of the likelihood function and the prior
distribution and ignoring the marginal distribution,