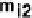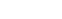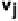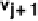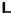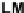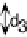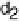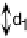Graphics Reference
In-Depth Information
Using the same argument as above, we can read off approximate values for the (con-
ditional) logarithms of the odds ratios log θ
and log θ
. Finding the difference be-
tween these logarithms of odds ratios then leads us to a generalization of odds ratios
to dimension three (Bhapkar and Koch,
):
log θ
−
log θ
=
log θ
θ
=
log θ
XY Z
.
Usinggroupconstraints, thethree-wayinteraction effectbetween X, Y and Z isequal
to the logarithm of the odds ratio:
λ
XY Z
log θ
XY Z
.
=
he absence of a three-way interaction therefore corresponds to θ
XY Z
, which
in turn corresponds to equal conditional odds ratios θ
and θ
. High-dimensional
interaction effects can be found visually in a similar fashion. his is explained in
more detail in Hofmann (
).
Forvariables with multiple categories, wewill supposethat at least oneof thevari-
ables of interest is binary. For a visual assessment of the interaction, we will use the
sameapproachasbefore.AnexampleisshowninFig.
.
,basedontheCollegePlans
data set (Sewell and Shah,
). Highlighted (marked in orange) are pupils whose
parents strongly encourage them to go to college. Highlighted heights show the con-
ditional probability of encouragement given a pupil's IQ. he percentage of parental
encouragement increases as the IQ increases. he increase in high parental encour-
agement with eachsuccessive IQlevel(denotedby d
, d
and d
)stays approximately
equal.
For multivariate contingency tables like the example, there are multiple ways of
obtaining odds ratios. A su
cient set of odds ratios, though, is the set of odds ratios
gained bycomputing the odds ratios of all quadruples of fouradjacent cells (see, e.g.,
Agresti,
).
=
Figure
.
.
Doubledecker plot of parental encouragement vs. IQ. Highlighting reveals an
approximately linear trend of encouragement vs. IQ